题目内容
设向量 =(0,2),
=(0,2), =(1,0),过定点A(0,-2),以
=(1,0),过定点A(0,-2),以 +λ
+λ 方向向量的直线与经过点B(0,2),以向量
方向向量的直线与经过点B(0,2),以向量 -2λ
-2λ 为方向向量的直线相交于点P,其中λ∈R,
为方向向量的直线相交于点P,其中λ∈R,
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)设过E(1,0)的直线l与C交于两个不同点M、N,求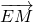 •
•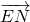 的取值范围.
的取值范围.
解:(Ⅰ)设P(x,y),∵ =(0,2),
=(0,2), =(1,0),∴
=(1,0),∴ +λ
+λ =(λ,2),
=(λ,2), -2λ
-2λ =(1,-4λ),
=(1,-4λ),
过定点A(0,-2),以 +λ
+λ 方向向量的直线方程为:2x-λy-2λ=0,
方向向量的直线方程为:2x-λy-2λ=0,
过定点B(0,2),以 -2λ
-2λ 方向向量的直线方程为:4λx+y-2=0,
方向向量的直线方程为:4λx+y-2=0,
联立消去λ得:8x2+y2=4∴求点P的轨迹C的方程为8x2+y2=4.
(Ⅱ)当过E(1,0)的直线l与x轴垂直时,l与曲线C无交点,不合题意,
∴设直线l的方程为:y=k(x-1),l与曲线C交于M(x1,y1),N(x2,y2),
由 ?(k2+8)x2-2k2x+k2-4=0,则
?(k2+8)x2-2k2x+k2-4=0,则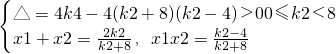 ,
,
又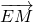 =(x1-1,y1),
=(x1-1,y1),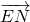 =(x2-1,y2),
=(x2-1,y2),
∴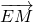 •
•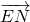 =(x1-1,y1)•(x2-1,y2)=x1x2-(x1+x2)+1+y1y2=x1x2-(x1+x2)+1+k2(x1-1)(x2-1)
=(x1-1,y1)•(x2-1,y2)=x1x2-(x1+x2)+1+y1y2=x1x2-(x1+x2)+1+k2(x1-1)(x2-1)
=(1+k2)x1x2-(1+k2)(x1+x2)+1+k2 =(1+k2)(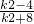 -
- +1)=
+1)= =4-
=4-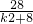 ,
,
∵0≤k2<8,∴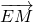 •
•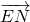 的取值范围是[
的取值范围是[ ,
, ).
).
分析:(Ⅰ)设P(x,y),求得过定点A(0,-2),以 +λ
+λ 方向向量的直线方程,以及过定点B(0,2),以
方向向量的直线方程,以及过定点B(0,2),以 -2λ
-2λ 方向向量的直线方程,消去λ即得点P的轨迹C的方程.
方向向量的直线方程,消去λ即得点P的轨迹C的方程.
(Ⅱ)用点斜式设直线l的方程,代入曲线C的方程得到根与系数的关系,判别式大于零,代入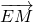 •
•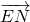 的式子化简,求得
的式子化简,求得 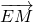 •
•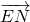 的取值范围.
的取值范围.
点评:本题考查求点的轨迹方程,一元二次方程根与系数的关系,两个向量的数量积公式,化简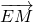 •
•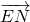 是解题的难点.
是解题的难点.
 =(0,2),
=(0,2), =(1,0),∴
=(1,0),∴ +λ
+λ =(λ,2),
=(λ,2), -2λ
-2λ =(1,-4λ),
=(1,-4λ),过定点A(0,-2),以
 +λ
+λ 方向向量的直线方程为:2x-λy-2λ=0,
方向向量的直线方程为:2x-λy-2λ=0,过定点B(0,2),以
 -2λ
-2λ 方向向量的直线方程为:4λx+y-2=0,
方向向量的直线方程为:4λx+y-2=0,联立消去λ得:8x2+y2=4∴求点P的轨迹C的方程为8x2+y2=4.
(Ⅱ)当过E(1,0)的直线l与x轴垂直时,l与曲线C无交点,不合题意,
∴设直线l的方程为:y=k(x-1),l与曲线C交于M(x1,y1),N(x2,y2),
由
 ?(k2+8)x2-2k2x+k2-4=0,则
?(k2+8)x2-2k2x+k2-4=0,则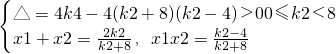 ,
,又
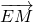 =(x1-1,y1),
=(x1-1,y1),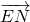 =(x2-1,y2),
=(x2-1,y2),∴
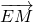 •
•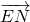 =(x1-1,y1)•(x2-1,y2)=x1x2-(x1+x2)+1+y1y2=x1x2-(x1+x2)+1+k2(x1-1)(x2-1)
=(x1-1,y1)•(x2-1,y2)=x1x2-(x1+x2)+1+y1y2=x1x2-(x1+x2)+1+k2(x1-1)(x2-1)=(1+k2)x1x2-(1+k2)(x1+x2)+1+k2 =(1+k2)(
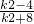 -
- +1)=
+1)= =4-
=4-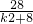 ,
,∵0≤k2<8,∴
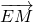 •
•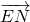 的取值范围是[
的取值范围是[ ,
, ).
).分析:(Ⅰ)设P(x,y),求得过定点A(0,-2),以
 +λ
+λ 方向向量的直线方程,以及过定点B(0,2),以
方向向量的直线方程,以及过定点B(0,2),以 -2λ
-2λ 方向向量的直线方程,消去λ即得点P的轨迹C的方程.
方向向量的直线方程,消去λ即得点P的轨迹C的方程.(Ⅱ)用点斜式设直线l的方程,代入曲线C的方程得到根与系数的关系,判别式大于零,代入
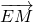 •
•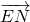 的式子化简,求得
的式子化简,求得 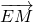 •
•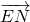 的取值范围.
的取值范围.点评:本题考查求点的轨迹方程,一元二次方程根与系数的关系,两个向量的数量积公式,化简
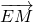 •
•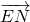 是解题的难点.
是解题的难点. 
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目