题目内容
15．方程lgx=2-x精确度0.1的近似根a≈1.8125；用a表示方程10x=2-x的一个根x=2-a．分析 作出y=lg x，y=2-x的图象，可以发现，方程lg x=2-x有唯一解，记为x0，并且解在区间（1，2）内．利用函数零点的判定定理即可得出．由于y=lgx与y=10x互为反函数，可得方程10x=2-x的一个根．
解答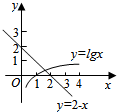 
解：作出y=lg x，y=2-x的图象，可以发现，方程lg x=2-x有唯一解，记为x0，并且解在区间（1，2）内．
设f（x）=lg x+x-2，用计算器计算
得f（1）＜0，f（2）＞0⇒x0∈（1，2）；
f（1.5）＜0，f（2）＞0⇒x0∈（1.5，2）；
f（1.75）＜0，f（2）＞0⇒x0∈（1.75，2）；
f（1.75）＜0，f（1.875）＞0⇒x0∈（1.75，1.875）；
f（1.75）＜0，f（1.812 5 ）＞0⇒x0∈（1.75，1.812 5）；
∵|1.812 5-1.75|=0.062 5＜0.1，
∴a≈1.812 5；
由y=x与y=2-x联立，可得x=y=1，由于y=lgx与y=10x互为反函数，可得方程10x=2-x的一个根x=2-a．
故答案为：1.812 5；2-a．
点评 熟练掌握函数零点的判定定理及二分法求函数零点的方法、数形结合思想是解题的关键．
练习册系列答案
相关题目
6．将y=f（x）图象上的每一点的纵坐标保持不变，横坐标变为原来的$\frac{1}{2}$，再将其图象沿x轴向左平称$\frac{π}{6}$个单位，得到的曲线与y=sin2x的图象相同，则f（x）的解析式为（ ）
| A． | y=sin（4x-$\frac{π}{3}$） | B． | y=sin（x-$\frac{π}{6}$） | C． | y=sin（4x+$\frac{π}{3}$） | D． | y=sin（x-$\frac{π}{3}$） |
10．函数y=x3-lnx在x=1处的切线方程为（ ）
| A． | 2x+y-1=0 | B． | 2x+y+1=0 | C． | 2x-y-1=0 | D． | 2x-y+1=0 |
20．用二分法求函数f（x）=2x-x3的零点，以下四个区间中，可以作为起始区间的是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |