题目内容
正方形ABCD的边长为2，在其内部取点P，则事件“△PAB、△PBC、△PCD、△PDA的面积均大于
”的概率是 ．
【答案】分析：点P在正方形内部，P到正方形一边的距离为d，连接P与正方形各顶点的三角形的面积为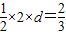
，知P到正方形四边的距离均大于
，从而确定出P所在的区域，用P点所在区域的面积除以正方形ABCD的面积即可．
解答：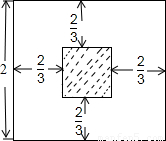
解：如图，点P在正方形ABCD内部，同时保证“△PAB、△PBC、△PCD、△PDA的面积均大于
”，则需要点P到正方形的四条边的距离均大于
，
即点P在正方形内部以
为边长的正方形区域内，且小正方形的每一条边到与它相邻的大正方形的边的距离为
，
其概率为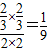
．
故答案为
．
点评：本题考查了几何概型，求几何概型的概率关键是看测度比是长度比还是面积比，亦或是体积比等，解答此题的关键是找到P点所在的区域，是基础题．
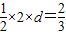，知P到正方形四边的距离均大于，从而确定出P所在的区域，用P点所在区域的面积除以正方形ABCD的面积即可．解答：
解：如图，点P在正方形ABCD内部，同时保证“△PAB、△PBC、△PCD、△PDA的面积均大于”，则需要点P到正方形的四条边的距离均大于，即点P在正方形内部以
为边长的正方形区域内，且小正方形的每一条边到与它相邻的大正方形的边的距离为，其概率为
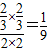．故答案为
．点评：本题考查了几何概型，求几何概型的概率关键是看测度比是长度比还是面积比，亦或是体积比等，解答此题的关键是找到P点所在的区域，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，正方形ABCD的边长为1，正方形ADEF所在平面与平面ABCD互相垂直，G，H是DF，FC的中点．