Question

双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的右支上存在一点，它到右焦点及左准线的距离相等，则双曲线离心率的取值范围是

(1，

2

+1]

．

Answer 1

分析：如图所示，设P（x，y）．由双曲线的第二定义可得

|PF2|

|PN|

=e，再利用已知和准线的定义可得|PF2|=|PM|=|PN|+

2a2

c

，进而得到|PN|+

2a2

c

=e|PN|．又|PN|=x-

a2

c

，代入化为x=

a(e+1)

e(e-1)

，利用点P在双曲线的右支上，可得x≥a，解出即可．

解答：解：如图所示，设P（x，y）．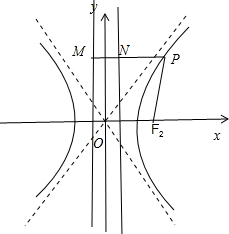
由双曲线的第二定义可得

|PF2|

|PN|

=e，
∵|PF2|=|PM|=|PN|+

2a2

c

，
∴|PN|+

2a2

c

=e|PN|．
∵|PN|=x-

a2

c

，代入化为x=

a(e+1)

e(e-1)

，
∵点P在双曲线的右支上，∴x≥a，
∴

a(e+1)

e(e-1)

≥a，化为e²-2e-1≤0，又e＞1，
解得1＜e≤1+

2

．
∴双曲线离心率的取值范围是(1，

2

+1]．
故答案为(1，

2

+1]．

点评：本题考查了双曲线的第二定义及其性质、离心率的取值范围、一元二次不等式的解法等基础知识与基本技能，属于中档题．