题目内容
二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,图象与x轴的两个交点中,一个交点的横坐标x1∈(2,3),则有
- A.abc>0
- B.a+b+c<0
- C.a+c>b
- D.3b<2c
C
分析:由二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,可以知道a<0,b=-2a,交点的横坐标x1∈(2,3),可得到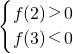 ,从而可得答案.
,从而可得答案.
解答:∵二次函数f(x)=ax2+bx+c的图象开口向下,
∴a<0,又对称轴为x=1,
∴x=- =1,
=1,
∴b=-2a;
∴f(x)=ax2-2ax+c.
又与x轴的两个交点中,一个交点的横坐标x1∈(2,3),a<0,
∴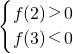 即:
即: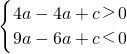 ,
,
∴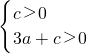 ,
,
∴a+c>-2a=b.C符合.
又a<0,b=-2a>0,c>0,
∴abc<0,排出A,
∵二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,
∴f(1)=a+b+c>0,排出B,f(-1)=f(3),
图象与x轴的两个交点中一个交点的横坐标x1∈(2,3),
∴f(-1)=f(3)<0,而f(-1)=a-b+c=- b+c<0,
b+c<0,
∴3b>2c,排出D.
故选C.
点评:本题考查了二次函数图象与性质,关键在于准确把握题目信息的意图,合理转化,特别是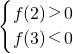 的分析与应用是难点.属于中档题.
的分析与应用是难点.属于中档题.
分析:由二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,可以知道a<0,b=-2a,交点的横坐标x1∈(2,3),可得到
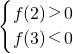 ,从而可得答案.
,从而可得答案.解答:∵二次函数f(x)=ax2+bx+c的图象开口向下,
∴a<0,又对称轴为x=1,
∴x=-
 =1,
=1,∴b=-2a;
∴f(x)=ax2-2ax+c.
又与x轴的两个交点中,一个交点的横坐标x1∈(2,3),a<0,
∴
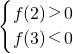 即:
即: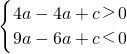 ,
,∴
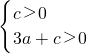 ,
,∴a+c>-2a=b.C符合.
又a<0,b=-2a>0,c>0,
∴abc<0,排出A,
∵二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,
∴f(1)=a+b+c>0,排出B,f(-1)=f(3),
图象与x轴的两个交点中一个交点的横坐标x1∈(2,3),
∴f(-1)=f(3)<0,而f(-1)=a-b+c=-
 b+c<0,
b+c<0,∴3b>2c,排出D.
故选C.
点评:本题考查了二次函数图象与性质,关键在于准确把握题目信息的意图,合理转化,特别是
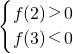 的分析与应用是难点.属于中档题.
的分析与应用是难点.属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +bx(a,b是常数且a
+bx(a,b是常数且a 0)满足条件:f(2)=0.方程f(x)=x有等根
0)满足条件:f(2)=0.方程f(x)=x有等根