题目内容
设函数f（x）定义在（0，+∞）上，f（1）=0，导函数f（x）=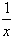
，g（x）=f（x）+f′（x），求g（x）的单调区间和最小值。
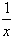，g（x）=f（x）+f′（x），求g（x）的单调区间和最小值。 解：由题设易知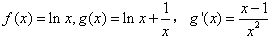
令g′（x）=0，得x=1，
当x∈（0，1）时，g′（x）＜0，故（0，1）是g（x）的单调减区间；
当x∈（1，+∞）时，g′（x）＞0 ，故（1，+∞）是g（x）的单调增区间，
因此，x=1是g（x）的唯一极值点，且为极小值点，从而是最小值点，
所以最小值为g（1）=1。
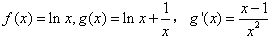
令g′（x）=0，得x=1，
当x∈（0，1）时，g′（x）＜0，故（0，1）是g（x）的单调减区间；
当x∈（1，+∞）时，g′（x）＞0 ，故（1，+∞）是g（x）的单调增区间，
因此，x=1是g（x）的唯一极值点，且为极小值点，从而是最小值点，
所以最小值为g（1）=1。
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目