Question

如图,在棱长为2的正方体ABCD—A₁B₁C₁D₁中,E是BC₁的中点,求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).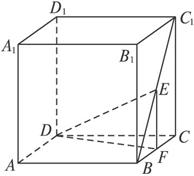

Answer 1

解:过E作EF⊥BC,交BC于F,连接DF.

∵EF⊥平面ABCD,

∴∠EDF是直线DE与平面ABCD所成的角.                                    

由题意,得EF==1.

∵CF==1,∴DF=.                                                    

∵EF⊥DF,∴tan∠EDF=.                                          

故直线DE与平面ABCD所成角的大小是arctan.