题目内容
【题目】已知函数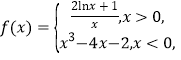 若方程
若方程![]() 有四个不等的实数根,则实数
有四个不等的实数根,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
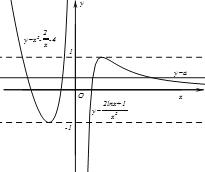
解法一:把方程![]() 有四个实数根,转化为函数
有四个实数根,转化为函数![]() 与
与![]() 图像有四个不同的交点.分别求得当
图像有四个不同的交点.分别求得当![]() 时,函数
时,函数![]() 单调性与极值和当
单调性与极值和当![]() 时,函数
时,函数![]() 单调性与极值,作出图象,结合图象即可求解;
单调性与极值,作出图象,结合图象即可求解;
解法二:由方程![]() 等价于
等价于![]() ,转化为
,转化为![]() 与
与![]() 图像有四个交点,令
图像有四个交点,令![]() ,分别求得当
,分别求得当![]() 和
和![]() 时,函数的单调性与极值,结合图象,即可求解.
时,函数的单调性与极值,结合图象,即可求解.
解法一:方程![]() 有四个实数根,
有四个实数根,
等价于![]() 与
与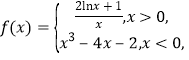 图像有四个不同的交点.
图像有四个不同的交点.
当![]() 时,
时,![]()
![]() 解得
解得![]() .
.
当![]() ,
,![]()
![]() 单调递增,
单调递增,
当![]() 时,
时,![]()
![]() 单调递减,所以
单调递减,所以![]() 极大值为
极大值为![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,![]() 解得
解得![]() (舍正),
(舍正),
当![]() 时,
时,![]()
![]() 单调递增,
单调递增,
当![]() 时,
时,![]()
![]() 单调递减,所以
单调递减,所以![]() 极大值为
极大值为![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
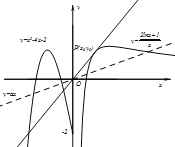
作出函数![]() 的草图,如图:
的草图,如图:
①若![]()
![]() 与
与![]() 不可能有四个交点;
不可能有四个交点;
②若![]()
![]() 与
与![]() 有三个交点;
有三个交点;
③若![]() 当
当![]() 与
与![]() 相切时,
相切时,
设切点为![]() 则
则![]() ,即
,即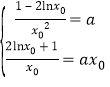
解得![]() ,两图像要有四个交点,则
,两图像要有四个交点,则![]() .
.
综上实数![]() 的取值范围是
的取值范围是![]() ,故选B.
,故选B.
解法二:由于![]() ,方程
,方程![]() 等价于
等价于![]() ,
,
即依题意![]() 与
与![]() 图像有四个交点.
图像有四个交点.
令![]() ,
,
当![]() ,
,![]()
![]() 得
得![]() .
.
当![]() 时
时![]()
![]() 单调递增,当
单调递增,当![]() 时,
时,![]()
![]() 单调递减,
单调递减,
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
又当![]() 时,
时,![]() 得
得![]() ,
,
当![]() 时,
时,![]()
![]() 单调递减,
单调递减,
当![]() 时,
时,![]()
![]() 单调递增,
单调递增,![]() 极小值为
极小值为![]() ,
,
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
所以![]() 与
与![]() 图像有四个交点时
图像有四个交点时![]() 故选B.
故选B.

【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.

(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【题目】“爱国,是人世间最深层、最持久的情感,是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中,爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造,根据市场调研与模拟,得到科技改造投入![]() (亿元)与科技改造直接收益
(亿元)与科技改造直接收益![]() (亿元)的数据统计如下:
(亿元)的数据统计如下:
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当![]() 时,建立了
时,建立了![]() 与
与![]() 的两个回归模型:模型①:
的两个回归模型:模型①:![]() ;模型②:
;模型②:![]() ;当
;当![]() 时,确定
时,确定![]() 与
与![]() 满足的线性回归方程为:
满足的线性回归方程为:![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①、②的相关指数
时模型①、②的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
(附:刻画回归效果的相关指数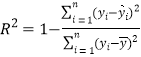 ,
,![]() .)
.)
(2)为鼓励科技创新,当科技改造的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较科技改造投入17亿元与20亿元时公司实际收益的大小;
(附:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式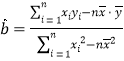
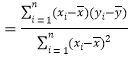 ;
;![]() )
)
(3)科技改造后,“东方红”款汽车发动机的热效![]() 大幅提高,
大幅提高,![]() 服从正态分布
服从正态分布![]() ,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过
,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过![]() ,不予奖励;若发动机的热效率超过
,不予奖励;若发动机的热效率超过![]() 但不超过
但不超过![]() ,每台发动机奖励2万元;若发动机的热效率超过
,每台发动机奖励2万元;若发动机的热效率超过![]() ,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
(附:随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .)
.)

