题目内容
已知等比数列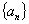 中各项均为正,有
中各项均为正,有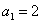 ,
,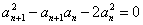 ,
,
等差数列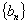 中,
中, ,点
,点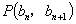 在直线
在直线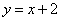 上.
上.
(1)求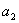 和
和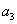 的值;(2)求数列
的值;(2)求数列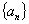 ,
,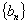 的通项
的通项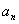 和
和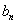 ;
;
(3)设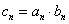 ,求数列
,求数列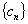 的前n项和
的前n项和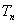 .
.
解:(1)∵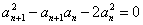
∴ ,又
,又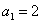
解得 ,
, (舍去)
(舍去)
 ,解得
,解得 ,
, (舍去)
(舍去)
(2)∵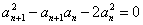
∴ ,
,
∵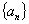 中各项均为正,∴
中各项均为正,∴
又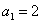 ∴即数列
∴即数列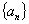 是以2为首项以为2公比的等比数列
是以2为首项以为2公比的等比数列
∴ ……6分
……6分
∵点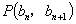 在直线
在直线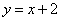 上,∴
上,∴ ,
,
又 ∴数列
∴数列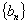 是以1为首项以为2公差的等差数列
是以1为首项以为2公差的等差数列
∴
(3)由(1)得
∴
=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
因此:-Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn= (2n-3)2n+1+6

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
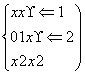 的值的程序框图,则在①、②和③处应分别填入的是( )
的值的程序框图,则在①、②和③处应分别填入的是( )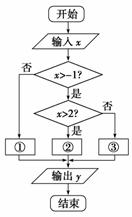
 和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为( )
和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为( )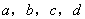 成等比数列,则
成等比数列,则 也成等比数列;②若数列{
也成等比数列;②若数列{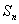 ,且
,且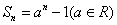 ,则{
,则{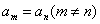 ,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上) 件产品中,有
件产品中,有 件合格品,
件合格品, 件次品.从这100件产品中任意抽取
件次品.从这100件产品中任意抽取 件,恰好有一件是次品的抽法有
件,恰好有一件是次品的抽法有  种 B、
种 B、 种 C、
种 C、 种 D、
种 D、 种
种 的直线与抛物线
的直线与抛物线 交于
交于 两点,且
两点,且 ,
, 为坐标原点,则该直线的方程为
为坐标原点,则该直线的方程为 B、
B、 C、
C、 D、
D、
 在区间
在区间 上的最小值是
上的最小值是  C.
C. D.0
D.0