题目内容
(2013•盐城二模)(选修4-5:不等式选讲)
若x∈(-
,
),证明
+
+
<3
.
若x∈(-
| 1 |
| 2 |
| 2 |
| 3 |
| 1+2x |
| 3+x |
| 2-3x |
| 2 |
分析:直接构造18=6×3=[(1+2x)+(3+x)+(2-3x)](1+1+1),利用柯西不等式证明即可.
解答:证明:因为18=6×3=[(1+2x)+(3+x)+(2-3x)](1+1+1),
由柯西不等式可得:
18=[(1+2x)+(3+x)+(2-3x)](1+1+1)≥(
•1+
•1+
•1)2…(7分)
又x∈(-
,
),
所以
+
+
<3
.…(10分)
由柯西不等式可得:
18=[(1+2x)+(3+x)+(2-3x)](1+1+1)≥(
| 1+2x |
| 3+x |
| 2-3x |
又x∈(-
| 1 |
| 2 |
| 2 |
| 3 |
所以
| 1+2x |
| 3+x |
| 2-3x |
| 2 |
点评:本题考查柯西不等式的证明方法的应用,构造柯西不等式是解题的关键.

练习册系列答案
相关题目
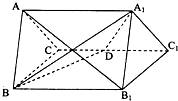 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.