题目内容
(本小题满分10分)
如图,在y轴的正半轴上依次有点 其中点
其中点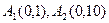 ,且
,且
 ,在射线
,在射线 上依次有
上依次有 点
点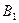 的坐
的坐 标为(3,3),且
标为(3,3),且


⑴用含 的式子表示
的式子表示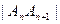 ;
;
⑵用含 的式子表示
的式子表示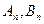 的坐标;
的坐标;
⑶求四边形 面积的最大值。
面积的最大值。
解:(1 )
) ,
,
(2)由(1)得
 的坐标
的坐标
 ,
,
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
(3)连接 ,设四边形
,设四边形
 的面积为
的面积为 ,则
,则



 单调递减.
单调递减. 的最大值为
的最大值为 .
.
解析

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
题目内容
(本小题满分10分)
如图,在y轴的正半轴上依次有点 其中点
其中点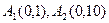 ,且
,且
 ,在射线
,在射线 上依次有
上依次有 点
点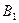 的坐
的坐 标为(3,3),且
标为(3,3),且


⑴用含 的式子表示
的式子表示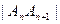 ;
;
⑵用含 的式子表示
的式子表示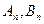 的坐标;
的坐标;
⑶求四边形 面积的最大值。
面积的最大值。
解:(1 )
) ,
,
(2)由(1)得
 的坐标
的坐标
 ,
,
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
(3)连接 ,设四边形
,设四边形
 的面积为
的面积为 ,则
,则



 单调递减.
单调递减. 的最大值为
的最大值为 .
.
解析

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案