题目内容
已知函数f(x)=ln(ex+a)(a为常数)是R上的奇函数.函数g(x)=λf(x)+sinx是区间[-1,1]上的减函数.
(1)讨论关于x的方程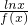 =x2-2ex+m的根的个数.
=x2-2ex+m的根的个数.
(2)若g(x)<t2+λt+1在x∈[-1,1]上恒成立,求t的取值范围.
解:(1)∵f(x)=ln(ex+a)是奇函数,∴f(x)+f(-x)=0即ln(ex+a)+ln(e-x+a)=0,即(ex+a)(e-x+a)=1,整理得a(e-x+ex+a)=0恒成立,故a=0 (1分)
又f(x)=x,由 =x2-2ex+m得
=x2-2ex+m得 ,
,
令f1(x)= ,f2(x)=x2-2ex+m…(2分)
,f2(x)=x2-2ex+m…(2分)
则f1′(x)= ,当x∈(0,e)时f1′(x)>0,f1(x)为增函数;当x∈(e,+∞)时f1′(x)<0,f1(x)为减函数,∴当x=e时,f1(x)的最小值为f1(e)=
,当x∈(0,e)时f1′(x)>0,f1(x)为增函数;当x∈(e,+∞)时f1′(x)<0,f1(x)为减函数,∴当x=e时,f1(x)的最小值为f1(e)=
而f2(x)=x2-2ex+m=(x-e)2-e2+m,结合f1(x)与f2(x)的大致图象可得
当-e2+m> 即 m>e2+
即 m>e2+ 时,方程无实根;当-e2+m=
时,方程无实根;当-e2+m= 即 m=e2+
即 m=e2+ 时,方程有一个实根;当-e2+m<
时,方程有一个实根;当-e2+m< 即 m<e2+
即 m<e2+ 时,方程有两个实根;
时,方程有两个实根;
(2)由题意可得:g(x)=λx+sinx,所以g'(x)=λ+cosx,由函数的单调性转化为:g'(x)=λ+cosx≤0 在[-1,1]上恒成立,进而得到λ≤-1,g(x)max=-λ-sin1,再转化为-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立.∴(t+1)λ+t2+sin1+1>0在λ∈(-∞,-1]上恒成立.
令h(λ)=(t+1)λ+t2+sin1+1,(λ≤-1)
则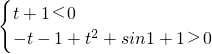 ,∴
,∴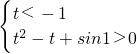 ,而t<-1时,t2-t+sin1>0恒成立,
,而t<-1时,t2-t+sin1>0恒成立,
经检验t=-1也对,∴t≤-1
分析:(1)函数f(x)=ln(ex+a)(a为常数)是实数集R上的奇函数,可得出f(x)+f(-x)=0,由此方程恒成立求a.构造两个函数f1(x)= ,f2(x)=x2-2ex+m,将方程有根的问题转化为函数有交点的问题进行研究.
,f2(x)=x2-2ex+m,将方程有根的问题转化为函数有交点的问题进行研究.
(2)由题意可得:g(x)=λx+sinx,所以g'(x)=λ+cosx,由函数的单调性转化为:g'(x)=λ+cosx≤0 在[-1,1]上恒成立,进而得到λ≤-1,并且g(x)max=-λ-sin1,再转化为-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立.把λ看为自变量利用一次函数的性质解决问题即可得到答案.
点评:本题考查导数在最大值与最小值问题中的应用,解答本题关键是掌握导数与单调性的关系,由函数的单调性判断出函数的最值,本题中第二问中的恒成立的问题就是一个求最值,利用最值建立不等式的题型,本类题运算量大,且多是符号运算,故解题时要严谨认真,避免因运算失误或变形失误导致解题失败.
又f(x)=x,由
 =x2-2ex+m得
=x2-2ex+m得 ,
,令f1(x)=
 ,f2(x)=x2-2ex+m…(2分)
,f2(x)=x2-2ex+m…(2分)则f1′(x)=
 ,当x∈(0,e)时f1′(x)>0,f1(x)为增函数;当x∈(e,+∞)时f1′(x)<0,f1(x)为减函数,∴当x=e时,f1(x)的最小值为f1(e)=
,当x∈(0,e)时f1′(x)>0,f1(x)为增函数;当x∈(e,+∞)时f1′(x)<0,f1(x)为减函数,∴当x=e时,f1(x)的最小值为f1(e)=
而f2(x)=x2-2ex+m=(x-e)2-e2+m,结合f1(x)与f2(x)的大致图象可得
当-e2+m>
 即 m>e2+
即 m>e2+ 时,方程无实根;当-e2+m=
时,方程无实根;当-e2+m= 即 m=e2+
即 m=e2+ 时,方程有一个实根;当-e2+m<
时,方程有一个实根;当-e2+m< 即 m<e2+
即 m<e2+ 时,方程有两个实根;
时,方程有两个实根;(2)由题意可得:g(x)=λx+sinx,所以g'(x)=λ+cosx,由函数的单调性转化为:g'(x)=λ+cosx≤0 在[-1,1]上恒成立,进而得到λ≤-1,g(x)max=-λ-sin1,再转化为-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立.∴(t+1)λ+t2+sin1+1>0在λ∈(-∞,-1]上恒成立.
令h(λ)=(t+1)λ+t2+sin1+1,(λ≤-1)
则
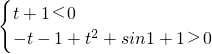 ,∴
,∴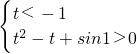 ,而t<-1时,t2-t+sin1>0恒成立,
,而t<-1时,t2-t+sin1>0恒成立,经检验t=-1也对,∴t≤-1
分析:(1)函数f(x)=ln(ex+a)(a为常数)是实数集R上的奇函数,可得出f(x)+f(-x)=0,由此方程恒成立求a.构造两个函数f1(x)=
 ,f2(x)=x2-2ex+m,将方程有根的问题转化为函数有交点的问题进行研究.
,f2(x)=x2-2ex+m,将方程有根的问题转化为函数有交点的问题进行研究.(2)由题意可得:g(x)=λx+sinx,所以g'(x)=λ+cosx,由函数的单调性转化为:g'(x)=λ+cosx≤0 在[-1,1]上恒成立,进而得到λ≤-1,并且g(x)max=-λ-sin1,再转化为-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立.把λ看为自变量利用一次函数的性质解决问题即可得到答案.
点评:本题考查导数在最大值与最小值问题中的应用,解答本题关键是掌握导数与单调性的关系,由函数的单调性判断出函数的最值,本题中第二问中的恒成立的问题就是一个求最值,利用最值建立不等式的题型,本类题运算量大,且多是符号运算,故解题时要严谨认真,避免因运算失误或变形失误导致解题失败.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目