题目内容

设f（x）=|4-x2|，若0＜m＜n，且f（m）=f（n），则m+n的取值范围是（　　）
A、（0，4）
B、（2
2
，4）
C、（0，2
2
）
D、（
2
，4）
分析：由题意f（x）=|4-x2|属于含绝对值的函数，利用绝对值的定义通过分类讨论的思想把绝对值脱去，转化为二次函数进行求解即可．
解答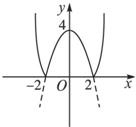：精英家教网解：y=f（x）=|4-x2|的图象如图．
∵0＜m＜n，f（m）=f（n），
∴0＜m＜2，n＞2．
∴4-m2=n2-4，即m2+n2=8．
∴
m2+n2=8
0＜m＜2
n＞2.

精英家教网∴点（m，n）轨迹为以（0，0）为圆心，以2
2
为半径的圆的一部分，如图
AB
．
设z=m+n，由线性规划知点Z为斜率为-1的直线与
AB
有公共点时在y轴上的截距，
∴直线过（0，2
2
）时，zmin=2
2
，过点（2，2）时，zmax=4．∴z∈（2
2
，4）．
点评：此题考查了利用绝对值的定义脱去绝对值，二次函数的对称性，动点的轨迹方程及利用数形结合的思想求解式子的最大值．
练习册系列答案
相关题目
14、某同学在借助计算器求“方程lgx=2-x的近似解（精确到0.1）”时，设f（x）=lgx+x-2，算得f（1）＜0，f（2）＞0；在以下过程中，他用“二分法”又取了4个x的值，计算了其函数值的正负，并得出判断：方程的近似解是x≈1.8．那么他再取的x的4个值分别依次是
1.5，1.75，1.875，1.8125
．
设f（x）的定义域为（0，+∞），对于任意正实数m，n恒有f（m•n）=f（m）+f（n），且当x＞1时，f(x)＞0，f(
1
2
)=-1．
（1）求f（2）的值；
（2）求证：f（x）在（0，+∞）上是增函数；
（3）解关于x的不等式f(x)≥2+f(
3
x-4
)．
已知f 1(x)=|3x-1|，f2(x)=|a•3x-9|(a＞0)，x∈R，且f（x）=
f1(x)，f1(x)≤f2(x)
f2(x)，f1(x)＞f2(x)

（1）当a=1时，求f（x）的解析式；
（2）在（1）的条件下，若方程f（x）-m=0有4个不等的实根，求实数m的范围；
（3）当2≤a＜9时，设f（x）=f2（x）所对应的自变量取值区间的长度为l（闭区间[m，n]的长度定义为n-m），试求l的最大值．
设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[-2，0）时，f（x）=(
2
2
)x-1，若在区间（-2，6）内的关于x的方程f（x）-logga（x+2）=0（a＞0且a≠1）恰有4个不同的实数根，则实数a的取值范围是（　　）
（2013•韶关一模）设f（x）在区间I上有定义，若对?x1，x2∈I，都有f(
x1+x2
2
)≥
f(x1)+f(x2)
2
，则称f（x）是区间I的向上凸函数；若对?x1，x2∈I，都有f(
x1+x2
2
)≤
f(x1)+f(x2)
2
，则称f（x）是区间I的向下凸函数，有下列四个判断：
①若f（x）是区间I的向上凸函数，则-f（x）在区间I的向下凸函数；
②若f（x）和g（x）都是区间I的向上凸函数，则f（x）+g（x）是区间I的向上凸函数；
③若f（x）在区间I的向下凸函数，且f（x）≠0，则
1
f(x)
是区间I的向上凸函数；
④若f（x）是区间I的向上凸函数，?x1，x2，x3，x4∈I，则有f（
x1+x2+x3+x4
4
）≥
f(x1)+f(x2)+f(x3)+f(x4)
4

其中正确的结论个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网