题目内容
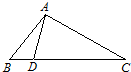
如图,△ABC中,∠ACB=90°,∠ABC=30°,BC= ,在三角形内挖去一个半圆(圆心O在边BC上,半圆与AC、AB分别相切于点C、M,与BC交于点N),求图中阴影部分绕直线BC旋转一周所得旋转体的体积。
,在三角形内挖去一个半圆(圆心O在边BC上,半圆与AC、AB分别相切于点C、M,与BC交于点N),求图中阴影部分绕直线BC旋转一周所得旋转体的体积。
 ,在三角形内挖去一个半圆(圆心O在边BC上,半圆与AC、AB分别相切于点C、M,与BC交于点N),求图中阴影部分绕直线BC旋转一周所得旋转体的体积。
,在三角形内挖去一个半圆(圆心O在边BC上,半圆与AC、AB分别相切于点C、M,与BC交于点N),求图中阴影部分绕直线BC旋转一周所得旋转体的体积。 
解:设半圆的半径为r,
在△ABC中,∠ACB=90°,∠ABC=30°, ,
,
连接OM,则OM⊥AB,
设OM=r,则OB=2r,
因为BC=OC+OB,所以BC=3r,
即 ,AC=BC·tan30°=1,
,AC=BC·tan30°=1,
阴影部分绕直线BC旋转一周所得旋转体为底面半径AC=1,高 的圆锥中间挖掉一个半径
的圆锥中间挖掉一个半径
 的球,
的球,
所以,V=V圆锥-V球= 。
。
在△ABC中,∠ACB=90°,∠ABC=30°,
 ,
,连接OM,则OM⊥AB,
设OM=r,则OB=2r,
因为BC=OC+OB,所以BC=3r,
即
 ,AC=BC·tan30°=1,
,AC=BC·tan30°=1,阴影部分绕直线BC旋转一周所得旋转体为底面半径AC=1,高
 的圆锥中间挖掉一个半径
的圆锥中间挖掉一个半径 的球,
的球,所以,V=V圆锥-V球=
 。
。 
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
 如图,
如图, 如图,△ABC中,
如图,△ABC中,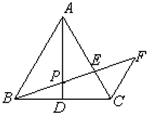 如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F, 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.