题目内容
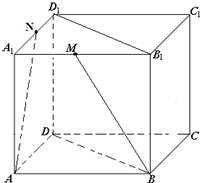 (文科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.
(文科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.(1)求异面直线AN与BM所成的角;
(2)求三棱锥M-DBB1的体积.
分析:(1)棱B1C1的中点为G,连接BG、GM、GN,先利用平行公理证明ABGN为平行四边形,再利用异面直线所成的角的定义证明∠MBG是异面直线AN与BM所成的角,最后在三角形中计算此角即可;
(2)先利用线面垂直的判定定理证明MH⊥平面DBB1D1,从而MH为三棱锥M-DBB1的高,再利用三棱锥的体积计算公式计算其体积即可
(2)先利用线面垂直的判定定理证明MH⊥平面DBB1D1,从而MH为三棱锥M-DBB1的高,再利用三棱锥的体积计算公式计算其体积即可
解答:解:(1)记棱B1C1的中点为G,连接BG、GM、GN,GM与B1D1的交点为H,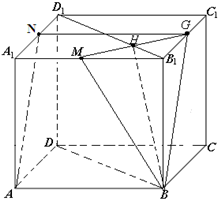
连接BH,如图所示.
∵ABCD-A1B1C1D1是正方体,G、N是中点,
∴GN∥A1B1∥AB,GN=A1B1=AB,即ABGN为平行四边形.
∴BG∥AN,
∴∠MBG是异面直线AN与BM所成的角.
在三角形MBG中,BM=BG=
a,MG=
a.
∴cos∠MBG=
=
异面直线AN与BM所成角为arccos
(2)∵B1H是等腰三角形MB1G的顶角平分线
∴BH⊥MH.
∵BB1⊥平面A1B1C1D1,MH?平面A1B1C1D1,∴BB1⊥MH.
∴MH⊥平面DBB1D1,即MH为三棱锥M-DBB1的高.
∴VM-DBB1=
•
•DB•BB1•MH=
•
a•a•
a=
a3

连接BH,如图所示.
∵ABCD-A1B1C1D1是正方体,G、N是中点,
∴GN∥A1B1∥AB,GN=A1B1=AB,即ABGN为平行四边形.
∴BG∥AN,
∴∠MBG是异面直线AN与BM所成的角.
在三角形MBG中,BM=BG=
| ||
| 2 |
| ||
| 2 |
∴cos∠MBG=
(
| ||||||||||||
2
|
| 4 |
| 5 |
异面直线AN与BM所成角为arccos
| 4 |
| 5 |
(2)∵B1H是等腰三角形MB1G的顶角平分线
∴BH⊥MH.
∵BB1⊥平面A1B1C1D1,MH?平面A1B1C1D1,∴BB1⊥MH.
∴MH⊥平面DBB1D1,即MH为三棱锥M-DBB1的高.
∴VM-DBB1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| ||
| 4 |
| 1 |
| 12 |
点评:本题主要考查了异面直线所成的角的定义及其作法、证法、算法,椎体的体积计算公式及其应用,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
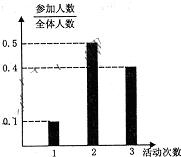 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
