题目内容
已知离心率为 的椭圆
的椭圆 (a>b>0)经过点
(a>b>0)经过点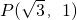 .
.
(1)求椭圆C的方程;
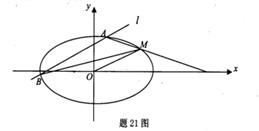
(2)过左焦点F1且不与x轴垂直的直线l交椭圆C于M、N两点,若 (O为坐标原点),求直线l的方程.
(O为坐标原点),求直线l的方程.
解:(1)依题意,离心率为 的椭圆
的椭圆 (a>b>0)经过点
(a>b>0)经过点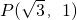 .
.
∴ ,且
,且
解得:a2=6,b2=2
故椭圆方程为 …(4分)
…(4分)
(2)椭圆的左焦点为F1(-2,0),则直线l的方程可设为y=k(x+2)
代入椭圆方程得:(3k2+1)x2+12k2x+12k2-6=0
设M(x1,y1),N(x2,y2),∴ ,
, …(6分)
…(6分)
由 得:
得: ,
,
∴ …(9分)
…(9分)
又 ,原点O到l的距离
,原点O到l的距离 ,
,
则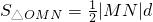 =
=
解得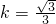
∴l的方程是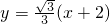 …(13分)
…(13分)
(用其他方法解答参照给分)
分析:(1)根据离心率为 的椭圆
的椭圆 (a>b>0)经过点
(a>b>0)经过点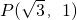 ,建立方程,确定几何量的值,从而可得椭圆方程;
,建立方程,确定几何量的值,从而可得椭圆方程;
(2)设直线l的方程代入椭圆方程得:(3k2+1)x2+12k2x+12k2-6=0,根据 ,可得
,可得 ,再利用
,再利用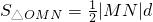 ,求得k的值,即可求得l的方程.
,求得k的值,即可求得l的方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确计算三角形的面积是关键.
 的椭圆
的椭圆 (a>b>0)经过点
(a>b>0)经过点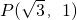 .
.∴
 ,且
,且
解得:a2=6,b2=2
故椭圆方程为
 …(4分)
…(4分)(2)椭圆的左焦点为F1(-2,0),则直线l的方程可设为y=k(x+2)
代入椭圆方程得:(3k2+1)x2+12k2x+12k2-6=0
设M(x1,y1),N(x2,y2),∴
 ,
, …(6分)
…(6分)由
 得:
得: ,
,∴
 …(9分)
…(9分)又
 ,原点O到l的距离
,原点O到l的距离 ,
,则
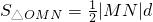 =
=
解得
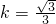
∴l的方程是
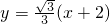 …(13分)
…(13分)(用其他方法解答参照给分)
分析:(1)根据离心率为
 的椭圆
的椭圆 (a>b>0)经过点
(a>b>0)经过点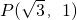 ,建立方程,确定几何量的值,从而可得椭圆方程;
,建立方程,确定几何量的值,从而可得椭圆方程;(2)设直线l的方程代入椭圆方程得:(3k2+1)x2+12k2x+12k2-6=0,根据
 ,可得
,可得 ,再利用
,再利用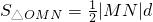 ,求得k的值,即可求得l的方程.
,求得k的值,即可求得l的方程.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确计算三角形的面积是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的椭圆C1的顶点A1,A2恰好是双曲线
的椭圆C1的顶点A1,A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.
的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2. 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值.
,求实数m的值.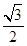 的椭圆
的椭圆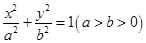 上的点到左焦点
上的点到左焦点 的最长距离为
的最长距离为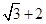 .
.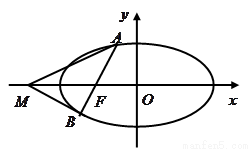
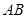 ,若点
,若点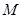 在
在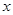 轴上,且使得
轴上,且使得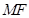 为
为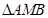 的一条内角平分线,则称点
的一条内角平分线,则称点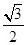 的椭圆
的椭圆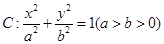 过点
过点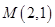 ,
,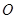 为坐标原点,平行于
为坐标原点,平行于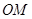 的直线
的直线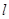 交椭圆于
交椭圆于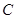 不同的两点
不同的两点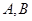 。
。
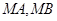 的斜率分别为
的斜率分别为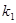 、
、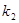 ,求证:
,求证: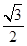 的椭圆
的椭圆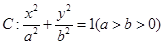 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线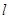 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;