题目内容
(本小题12分)已知 满足
满足 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;
(2)已知 三个内角
三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,且
,且 ,求
,求 面积的最大值.
面积的最大值.
 满足
满足 .
.(1)将
 表示为
表示为 的函数
的函数 ,并求
,并求 的单调递增区间;
的单调递增区间;(2)已知
 三个内角
三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若 ,且
,且 ,求
,求 面积的最大值.
面积的最大值.(1) 即为
即为 的单调递增区间.
的单调递增区间.
(2) 面积的最大值为
面积的最大值为
 即为
即为 的单调递增区间.
的单调递增区间. (2)
 面积的最大值为
面积的最大值为
(1)根据数量积的坐标表示建立关于x,y的等式关系,再借助两角和与差的正余弦公式化简可得f(x)的表达式。
(2)先求 ,确定出角A的大小,再根据a=2,利用余弦定理可知
,确定出角A的大小,再根据a=2,利用余弦定理可知
 ,从而求出bc的最大值,进而得到面积的最大值。
,从而求出bc的最大值,进而得到面积的最大值。
解:(1)
 所以
所以 ,………………………3分
,………………………3分
令 ,得
,得 即为
即为 的单调递增区间. ………………6分
的单调递增区间. ………………6分
(2) 又
又
 ………………………………8分
………………………………8分
在 中由余弦定理有,
中由余弦定理有,
可知 (当且仅当
(当且仅当 时取等号),
时取等号),
即 面积的最大值为
面积的最大值为 ………………………………12分
………………………………12分
(2)先求
 ,确定出角A的大小,再根据a=2,利用余弦定理可知
,确定出角A的大小,再根据a=2,利用余弦定理可知 ,从而求出bc的最大值,进而得到面积的最大值。
,从而求出bc的最大值,进而得到面积的最大值。解:(1)

 所以
所以 ,………………………3分
,………………………3分令
 ,得
,得 即为
即为 的单调递增区间. ………………6分
的单调递增区间. ………………6分(2)
 又
又
 ………………………………8分
………………………………8分在
 中由余弦定理有,
中由余弦定理有,
可知
 (当且仅当
(当且仅当 时取等号),
时取等号),
即
 面积的最大值为
面积的最大值为 ………………………………12分
………………………………12分
练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
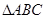 中,
中,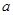 、
、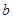 、
、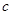 分别是角
分别是角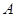 、
、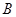 、
、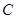 的对边,若
的对边,若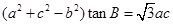 ,则角
,则角 ,设
,设 =
= (1).求
(1).求 的方程
的方程 在
在 有两个不相等的实数根,求
有两个不相等的实数根,求 与
与 成正比,与距离
成正比,与距离 的平方成反比,即
的平方成反比,即 ,设电灯可沿着BO移动,为了使水平面上的点A 处获得最大的亮度,则
,设电灯可沿着BO移动,为了使水平面上的点A 处获得最大的亮度,则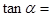 。
。
 中,边
中,边 所对的角分别是
所对的角分别是 ,下列结论正确的是 。
,下列结论正确的是 。 ,则
,则 ; ② 若
; ② 若 ,则
,则 ; ④
; ④  ,则
,则 .
. 的值域为
的值域为


 ( )
( )



 ,
, ,则
,则 ( )
( )



 ,且
,且 ,则
,则 ________.
________.