题目内容
在等差数列{an}中,若a3+a8+a13=12,a3a8a13=28.求:{an}的通项公式.
解:设所求的通项公式为an=a1+(n-1)d,则
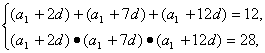
即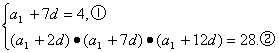
由①②得(a1+2d)(a1+12d)=7,③
由①③得d=±![]() .
.
当d=![]() 时,a1=
时,a1=![]() ,
,
an=![]() +(n-1)·
+(n-1)·![]() =
=![]() n-
n-![]() ;
;
当d=![]() 时,a1=
时,a1=![]() ,an=
,an=![]() +(n-1)·(
+(n-1)·(![]() )=
)=![]() n+
n+![]() .
.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
题目内容
在等差数列{an}中,若a3+a8+a13=12,a3a8a13=28.求:{an}的通项公式.
解:设所求的通项公式为an=a1+(n-1)d,则
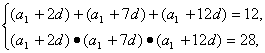
即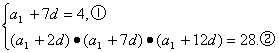
由①②得(a1+2d)(a1+12d)=7,③
由①③得d=±![]() .
.
当d=![]() 时,a1=
时,a1=![]() ,
,
an=![]() +(n-1)·
+(n-1)·![]() =
=![]() n-
n-![]() ;
;
当d=![]() 时,a1=
时,a1=![]() ,an=
,an=![]() +(n-1)·(
+(n-1)·(![]() )=
)=![]() n+
n+![]() .
.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案