题目内容

已知函数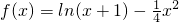 $数学公式$
（1）讨论函数f（x）的单调区间；
（2）求函数f（x）在[0，2]上的最大值和最小值．

解：（1） $\text{[math]}$ …（3分）
所以，x∈（-1，1）时递增，（1，+∞）递减．…（4分）
（2）x∈（0，，1）时递增，（1，2）递减
∵f（0）=0， $\text{[math]}$ ，…（6分）
所以，f（x）最大值= $\text{[math]}$ ，f（x）最小值=f（0）=0．…（4分）
分析：（1）先求导函数 $\text{[math]}$ ，再根据导数大于0，得函数的增区间，导数小于0，得函数的减区间；
（2）在（1）的基础上知函数在x∈（0，，1）时递增，（1，2）递减，从而可求函数的最大值和最小值．
点评：本题主要考查利用导数求函数的单调区间及函数在区间上的最值，属于基础题．

练习册系列答案

名师手把手系列答案

星际培优测试系列答案

新编助学读本系列答案

数学课堂与感悟系列答案

单元双测专题期中期末大试卷系列答案

金点考单元同步检测系列答案

素质目标检测系列答案

每课100分系列答案

智慧学习导学练系列答案

学科王同步课时练习系列答案

相关题目

已知函数函f（x）=x|x|-2x （x∈R）
（1）判断函数的奇偶性，并用定义证明；
（2）作出函数f（x）=x|x|-2x的图象；
（3）讨论方程x|x|-2x=a根的情况．

已知函数函f（x）=x|x|-2x　（x∈R）
（1）判断函数的奇偶性，并用定义证明；
（2）作出函数f（x）=x|x|-2x的图象；
（3）讨论方程x|x|-2x=a根的情况．

已知函数f(x)=log_a(a^x-1)(a＞0且a≠1)，
(1)求f(x)的定义域；
(2)讨论f(x)的单调性；
(3)x为何值时，函数值大于1。

已知函数f(x)=log_a(a^x-1)(a＞0且a≠1).

(1)求f(x)的定义域；

(2)当x为何值时，函数值大于1；

(3)讨论f(x)的单调性；

(4)解方程f(2x)=f^-1(x).

已知函数f(x)=log_a(a^x-1)(a＞1).

(1)求f(x)的定义域;

(2)当x为何值时,函数值大于1;

(3)讨论f(x)的单调性;

(4)解方程f(2x)=f^-1(x).