Question

在四边形ABCD中，AB=CD，BC=AD（如图所示），求证：ABCD为平行四边形，写出三段论形式的演绎推理。

Answer 1

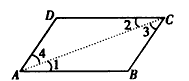
证明：（1）连接AC；
（2）平面几何中的三角形“边边边”定理有：有三边对应相等的两个三角形全等，这一定理相当于： 对于任意两个三角形，如果它们的三边对应相等，则这两个三角形全等， 大前提；
△ABC和△CDA的三边对应相等，小前提；
则这两个三角形全等，结论；
符号表示：；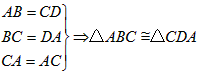
（3）由全等三角形的定义可知：全等三角形的对应角相等，这一性质相当于：对于任意两个三角形，如果它们全等，则它们的对应角相等，大前提；
△ABC和△CDA全等，小前提；
则它们的对应角相等，结论；
用符号表示，就是△ABC≌△CDA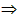∠1=∠2且∠3=∠4 且∠B=∠D；
（4）两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行，大前提；
直线AB、DC被直线AC所截，内错角∠1=∠2，小前提；
则AB∥DC，结论；
同理有：BC∥AD；
（5）如果四边形两组对边分别平行，那么这个四边形是平行四边形，大前提；
四边形ABCD中，两组对边分别平行，小前提；
则四边形ABCD是平行四边形，结论；
用符号表示为：AB∥DC且AD∥BC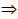四边形ABCD为平行四边形。