题目内容
等比数列{an}的各项均为正数,且a2与a4的等比中项为(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}满足b1=1,且bn+1=bn+an,求数列{bn}的通项公式.
解:(Ⅰ)依题意得:a2a4=(![]() )2,
)2,
又∵![]() =a2a4,a3>0.∴a3=
=a2a4,a3>0.∴a3=![]()
∵a2+a3=2×![]() ,∴a2=
,∴a2=![]() ,
,
故公比q=![]() ,a1=1. an=a1qn-1=21-n,
,a1=1. an=a1qn-1=21-n,
即{an}的通项公式为an=a1qn-1=21-n
(Ⅱ)∵bn+1=bn+an(n=1,2,3,…),
∴bn+1-bn=(![]() )n-1
)n-1
得b2- b1=1,
b3-b2=![]() ,
,
b4-b3=(![]() )2,
)2,
…,
bn-bn-1=(![]() )n-2
)n-2
各式相加得:bn- b1=1+![]() +(
+(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n-2
)n-2
=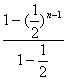 =2-2(
=2-2(![]() )n-1
)n-1
又∵b1=1,∴bn=3-(![]() )n-2
)n-2

练习册系列答案
相关题目
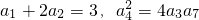 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .