题目内容
已知函数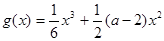 ,h(x)=2alnx,
,h(x)=2alnx,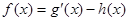 .
.
(1)当a∈R时,讨论函数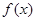 的单调性;
的单调性;
(2)是否存在实数a,对任意的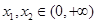 ,且
,且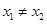 ,都有
,都有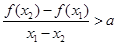
恒成立,若存在,求出a的取值范围;若不存在,说明理由.
【答案】
(1)详见解析;(2)不存在.
【解析】
试题分析:(1)讨论函数的单调性,在定义域内研究其导函数的符号即可.先求导函数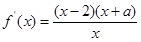
,因为定义域为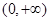 ,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点
,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点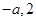 的大小,②注意根与定义域比较,所以
的大小,②注意根与定义域比较,所以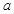 需和-2和0比较大小;(2)由对称性,不妨设
需和-2和0比较大小;(2)由对称性,不妨设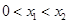 ,去分母得
,去分母得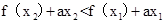 ,构造函数
,构造函数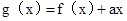 ,则其在定义域内单调递减,故
,则其在定义域内单调递减,故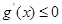 在
在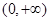 恒成立,而
恒成立,而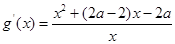 ,分子二次函数开口向上,不可能永远小于0,故不存在.
,分子二次函数开口向上,不可能永远小于0,故不存在.
试题解析:(1) 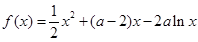 ,∴
,∴
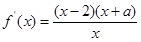 ,
, 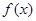 的定义域为
的定义域为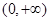 .
.
①当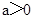 时,
时,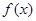 在
在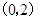 上是减函数,在在
上是减函数,在在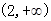 上是增函数;
上是增函数;
②当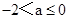 时,
时,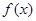 在
在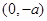 上是增函数;在
上是增函数;在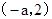 是是减函数;在
是是减函数;在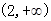 上是增函数;
上是增函数;
③当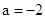 时,
时,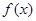 在
在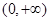 上是增函数;
上是增函数;
④当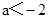 时,
时,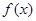 在
在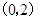 上是增函数;在
上是增函数;在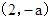 上是减函数;在
上是减函数;在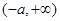 上是增函数.
上是增函数.
(2)假设存在实数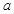 ,对任意的
,对任意的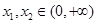 ,且
,且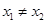 ,都有
,都有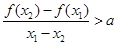 恒成立,不妨设
恒成立,不妨设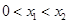 ,要使
,要使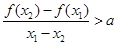 ,即
,即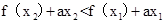 .
.
令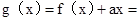
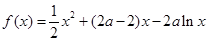 ,只要
,只要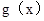 在
在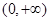 为减函数.
为减函数.
又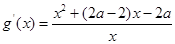 ,由题意
,由题意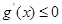 在
在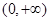 上恒成立,得
上恒成立,得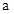 不存在.
不存在.
考点:1、导数在单调性上的应用;2、二次函数的图象;3、函数思想的应用.

练习册系列答案
相关题目
已知函数y=f(x)在点f(x)处可导,则
=( )
| lim |
| h→0 |
| f(x0+3h)-f(x0-2h) |
| h |
| A、f'(x0) | ||
| B、3f'(x0) | ||
C、
| ||
| D、5f'(x0) |
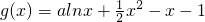 和h(x)=1-ax,其中a≤1且a≠0,设f(x)=g(x)+h(x).
和h(x)=1-ax,其中a≤1且a≠0,设f(x)=g(x)+h(x).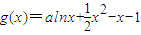 和h(x)=1-ax,其中a≤1且a≠0,设f(x)=g(x)+h(x).
和h(x)=1-ax,其中a≤1且a≠0,设f(x)=g(x)+h(x).