题目内容

设矩形ABCD在第一象限内，顶点A，B，C分别在函数 $数学公式$ 的图象上，且AB∥x轴，AD∥y轴，若点A的纵坐标为2，则点D的坐标为________．

$\text{[math]}$
分析：分别求出点A、B、C的坐标，然后再由矩形的边与坐标轴的位置关系，可求出点D坐标
解答：∵点A在y=-2log₂x上，且纵坐标为2
∴-2log₂x=2
∴x= $\text{[math]}$
∴点A的坐标为 $\text{[math]}$
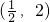
∴由题意点D的横坐标为 $\text{[math]}$
又∵AB∥x轴，且点B在 $\text{[math]}$ 上
∴点B的纵坐标为2，即 $\text{[math]}$
∴x=4
∴点B坐标为（4，2）
又∵四边形ABCD是矩形
∴BC∥y轴
∴点C的横坐标为4
又点C在 $\text{[math]}$ 上
∴点C的纵坐标为 $\text{[math]}$
∴由题意点D的纵坐标为 $\text{[math]}$
∵AD∥y轴
∴点D的横坐标为 $\text{[math]}$
∴点D的坐标为 $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考查指数式、对数式、幂指数的运算，须熟练应用运算律．属简单题

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

设矩形ABCD在第一象限内，顶点A，B，C分别在函数y=-2log2x，y=

，y=(

)x的图象上，且AB∥x轴，AD∥y轴，若点A的纵坐标为2，则点D的坐标为

如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、

PC的中点．

（1）求证：EF∥平面PAD；

（2）求证：EF⊥CD；

（3）若ÐPDA＝45°求EF与平面ABCD所成的角的大小．

【解析】本试题主要考查了线面平行和线线垂直的运用，以及线面角的求解的综合运用

第一问中，利用连AC，设AC中点为O，连OF、OE在△PAC中，∵ F、O分别为PC、AC的中点 ∴ FO∥PA …………①在△ABC中，∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD∵ EF Ì 平面EFO ∴ EF∥平面PAD．

第二问中在矩形ABCD中，∵ EO∥BC，BC⊥CD ∴ EO⊥CD 又 ∵ FO∥PA，PA⊥平面AC ∴ FO⊥平面AC∴ EO为EF在平面AC内的射影 ∴ CD⊥EF．

第三问中，若ÐPDA＝45°，则 PA＝AD＝BC ∵ EOBC，FOPA