Question

已知一个5次多项式为f（x）=5x⁵+2x⁴+3.5x³-2.6x²+1.7x-0.8，

    用秦九韶算法求这个多项式当x=5时的值.

Answer 1

解：根据秦九韶算法，把多项式改写成如下形式：

f(x)=（(((5x+2)x+3.5)x-2.6)x+1.7)x-0.8，

按照从内到外的顺序，依次计算一次多项式当x=5时的值：

v₀=5；

v₁=5×5+2=27;

v₂=27×5+3.5=138.5;

v₃=138.5×5-2.6=689.9;

v₄=689.9×5+1.7=3 451.2;

v₅=3 415.2×5-0.8=17 255.2;

所以，当x=5时，多项式的值等于17 255.2.

算法分析：观察上述秦九韶算法中的n个一次式，可见v_k的计算要用到v_k-1的值，若令v₀=a_n，我们可以得到下面的公式：

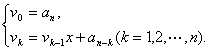
这是一个在秦九韶算法中反复执行的步骤，因此可用循环结构来实现.

算法步骤如下：

第一步，输入多项式次数n、最高次的系数a_n和x的值.

第二步，将v的值初始化为a_n，将i的值初始化为n-1.

第三步，输入i次项的系数a_i.

第四步，v=vx+a_i,i=i-1.

第五步，判断i是否大于或等于0.若是，则返回第三步；否则，输出多项式的值v.

程序框图如下图：

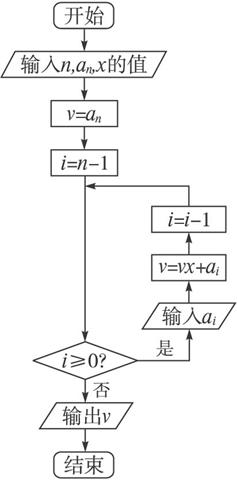
程序：

INPUT “n=”；n

INPUT “an=”；a

INPUT “x=”；x

v=a

i=n-1

WHILE i＞=0

  PRINT “i=”；i

  INPUT “ai=”；a

  v=v*x+a

  i=i-1

WEND

PRINT v

END

点评：本题是古老算法与现代计算机语言的完美结合，详尽介绍了思想方法、算法步骤、程序框图和算法语句,是一个典型的算法案例.