题目内容
已知三角形ABC的面积
，则角C的大小为（ ）A．30°
B．45°
C．60°
D．75°
【答案】分析：由余弦定理可得，三角形ABC的面积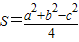
=
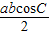，又S=
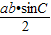，故sin C=cosC，
根据0＜C＜π，求出C的值．
解答：解：∵由余弦定理可得，三角形ABC的面积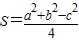
=
=
．
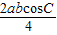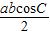又三角形ABC的面积 S=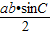
，∴sin C=cosC，再由 0＜C＜π，
可得 C=45°，
故选 B．
点评：本题考查余弦定理的应用，根据三角函数的值求角，求出sin C=cosC，是解题的关键．
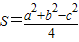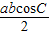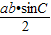=，又S=，故sin C=cosC，根据0＜C＜π，求出C的值．
解答：解：∵由余弦定理可得，三角形ABC的面积
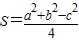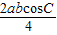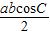==．又三角形ABC的面积 S=
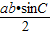，∴sin C=cosC，再由 0＜C＜π，可得 C=45°，
故选 B．
点评：本题考查余弦定理的应用，根据三角函数的值求角，求出sin C=cosC，是解题的关键．
练习册系列答案
相关题目
如图，已知四面体ABCD的四个面均为锐角三角形，EFGH分别是边AB，BC，CD，DA上的点，BD||平面EFGH，且EH=FG．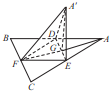
如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题：
），顶点C在
轴
与Rt△ABC外接圆相切于第一象限，求切线与两坐标轴所围成的三角形面