Question

素材1：过抛物线y²=2px(p＞0)的焦点F作直线l，交抛物线于A、B两点；

素材2：点C在抛物线的准线上，且BC∥x轴.

试据上述素材构建一个问题，然后再解答.

Answer 1

构建问题：过抛物线y²=2px(p＞0)的焦点F作直线l，交抛物线于A、B两点，点C在准线上，且BC∥x轴,试证明直线AC过原点O.

证明：由抛物线方程知焦点为F(p2,0)，设直线l的方程为x=my+

p2,代入y²=2px得y²-2pmy-p²=0.

设点A（x₁,y₁）、B（x₂,y₂）, 则y₁·y₂=-p².

∵BC∥x轴，且C点在准线上

∴C(-,y₂).

∴k_OC=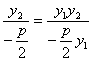

=

=

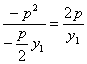
=k_OA.

∴A、O、C三点共线的直线AC经过原点O.

温馨提示

    设直线方程时，有y=kx+b和x=my+r两种形式，采用什么形式应根据题目条件.证法一中的结论：过焦点的直线l交抛物线y²=2px于A(x₁,y₁)和B(x₂,y₂)两点，则y₁·y₂=-p²可以作为一个定理记住.便于在解题中运用.