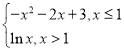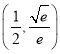题目内容
【题目】已知椭圆C:
（
）的左顶点为A，离心率为
，点
在椭圆C上.
（1）求椭圆C的方程；
（2）若直线
（
）与椭圆C交于E，F两点，直线
，
分别与y轴交于点M，N，求证:在x轴上存在点P，使得无论非零实数k怎样变化，以
为直径的圆都必过点P，并求出点P的坐标.
【答案】（1）
（2）证明见解析，
或
【解析】
（1）由题，得
，
，解方程组即可得到本题答案；
（2）联立直线方程与椭圆方程，求得直线
的方程，然后可以确定点
的坐标，由 
得方程，求解即可得到本题答案.
（1）依题意，
，所以①，又因为点
在椭圆
上，所以②，由①②解得
，
，所以椭圆方程为；
（2）假设存在这样的点P，设
，
，
，则
，联立
，消去y，得
，解得
，
， 因为
，所以
所在直线方程为
， 可得
，同理可得
，
所以
，
，
则
，解得
或
，所以存在点P且坐标为或，使得无论非零实数
怎么变化，以
为直径的圆都必过点P.
练习册系列答案
相关题目
【题目】一种室内种植的珍贵草药的株高
(单位:
)与一定范围内的温度
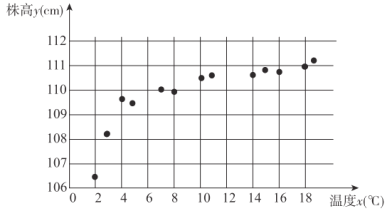
(单位:
)有关，现收集了该种草药的13组观测数据，得到如下的散点图，现根据散点图利用
或
建立关于的回归方程,令
,
,得到如下数据,且
与
(
)的相关系数分别为
,且
.
|
|
|
|
10.15 | 109.94 | 3.04 | 0.16 |
|
|
|
|
|
|
|
|
|
|
（1）用相关系数说明哪种模型建立与的回归方程更合适;
（2）根据（1）的结果及表中数据,建立
关于的回归方程;
（3）已知这种草药的利润
与,的关系为
，当为何值时，利润的预报值最大.
附:参考公式和数据:对于一组数据
（
）,其回归直线
的斜率和截距的最小二乘估计分别为
,
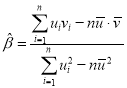,相关系数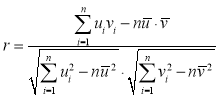
,
