题目内容
(本小题10分)已知函数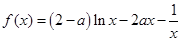 .
.
(1)试讨论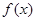 的单调性;
的单调性;
(2)如果当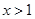 时,
时,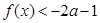 ,求实数
,求实数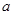 的取值范围;
的取值范围;
(3)记函数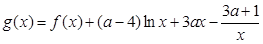 ,若
,若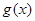 在区间
在区间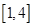 上不单调, 求实数
上不单调, 求实数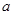 的取值范围.
的取值范围.
【答案】
解:(1)①若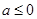 ,则
,则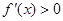 ,所以
,所以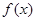 在
在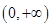 上单调递增
上单调递增
②若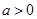 ,则由
,则由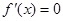 ,得
,得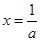 ,且当
,且当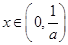 时,
时,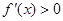 ,当
,当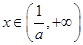 时,
时,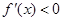 ,所以
,所以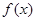 在
在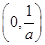 上单调递增,在
上单调递增,在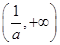 上单调递减;
上单调递减;
(2)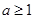 ;(3)
;(3)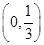 .
.
【解析】本试题主要是考查了导数在研究函数中的运用。解决不等式的恒成立问题,和函数的单调性的逆向运用的综合试题。
(1)首先求解导数,根据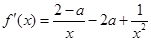
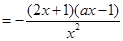 的分子为含有参数的二次函数,那么结合二次不等式进行分情况讨论得到单调区间。
的分子为含有参数的二次函数,那么结合二次不等式进行分情况讨论得到单调区间。
(2)利用当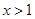 时,
时,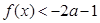 ,结合上一问的单调性,确定最值,解得a的范围。
,结合上一问的单调性,确定最值,解得a的范围。
(3)利用等价转化思想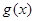 在区间
在区间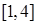 上不单调
上不单调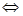
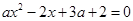
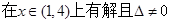 ,然后分离变量求解参数的取值范围。
,然后分离变量求解参数的取值范围。
解:(1)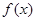 的定义域为
的定义域为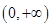 ,
,
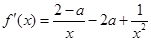
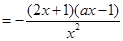 ……2分
……2分
①若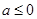 ,则
,则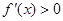 ,所以
,所以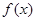 在
在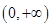 上单调递增
上单调递增
②若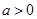 ,则由
,则由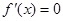 ,得
,得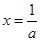 ,且当
,且当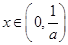 时,
时,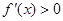 ,当
,当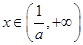 时,
时,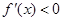 ,所以
,所以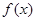 在
在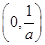 上单调递增,在
上单调递增,在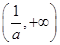 上单调递减;
……4分
上单调递减;
……4分
(2)由(1)知:
①若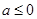 时,
时,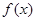 在
在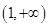 上单调递增,所以
上单调递增,所以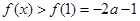 ,不合;
,不合;
②若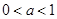 时,
时,
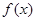 在
在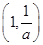 上单调递增,在
上单调递增,在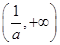 上单调递减;所以
上单调递减;所以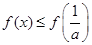 ,又
,又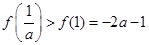 ,不合;
,不合;
③若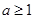 时,
时,
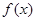 在
在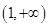 上单调递减;所以
上单调递减;所以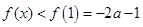 ,
,
综上所述,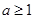 …………7分
…………7分
(3)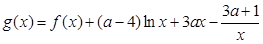
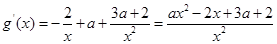
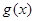 在区间
在区间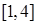 上不单调
上不单调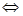
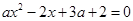
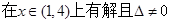
变量分离得,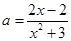
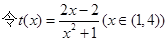 ,求得
,求得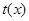 的值域为
的值域为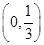
 ……10分
……10分

练习册系列答案
相关题目
 ,
,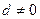 ,
,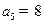 ,且项
,且项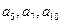 分别是某一等比数列
分别是某一等比数列 中的第
中的第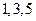 项,(1)求数列
项,(1)求数列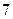 项。
项。
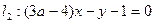 且
且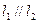 ,求以N(1,1)为圆心,并且与
,求以N(1,1)为圆心,并且与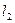 相切的圆的方程.
相切的圆的方程.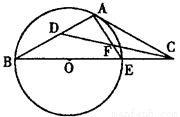
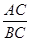 的值.
的值.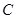 经过
经过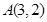 、
、 两点,且圆心在直线
两点,且圆心在直线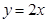 上.
上.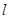 经过点
经过点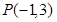 且与圆
且与圆 ,
, ;
; .
.