题目内容
命题P：?x∈Z，x3＜1．则¬P为 ．
【答案】分析：根据命题p：“?x∈Z，x3＜1．”是特称命题，其否定为全称命题，将“存在”改为“任意的”，“＜“改为“≥”即可得答案．
解答：解：∵命题p：“?x∈Z，x3＜1．”是特称命题
∴¬p：?x∈Z，x3≥1
故答案为：?x∈Z，x3≥1．
点评：本题主要考查全称命题与特称命题的相互转化问题．这里注意全称命题的否定为特称命题，反过来特称命题的否定是全称命题．属基础题．
解答：解：∵命题p：“?x∈Z，x3＜1．”是特称命题
∴¬p：?x∈Z，x3≥1
故答案为：?x∈Z，x3≥1．
点评：本题主要考查全称命题与特称命题的相互转化问题．这里注意全称命题的否定为特称命题，反过来特称命题的否定是全称命题．属基础题．
练习册系列答案
名校课堂系列答案
相关题目
命题p：?x∈R，|x+1|+k＜x，命题q：?x＞0，y＞0，z＞0＞且x+y+z=1，有k≤
+
+
．若“p∧q”为真，则实数K的取值范围是（ ）
| 1 |
| x |
| 2 |
| y |
| 1 |
| z |
A、[-1，6+4
| ||
B、[1，6+4
| ||
| C、[-1，16] | ||
| D、[1，16] |
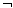q同时是假命题，则满足条件的x的集合为
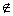Z}