题目内容
已知椭圆C的左、右焦点分别为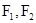 ,椭圆的离心率为
,椭圆的离心率为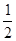 ,且椭圆C经过点
,且椭圆C经过点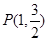 .
.
(1)求椭圆C的标准方程;
(2)若线段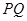 是椭圆过点
是椭圆过点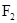 的弦,且
的弦,且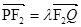 ,求
,求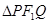 内切圆面积最大时实数
内切圆面积最大时实数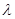 的值.
的值.
(1)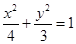 ;(2)
;(2)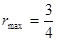 ,
,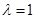 .
.
解析试题分析:本题主要考查直线、椭圆的标准方程及其性质,考查思维能力,运算能力.第一问,利用离心率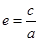 和椭圆过定点
和椭圆过定点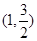 求椭圆的标准方程;第二问,分两种情况:当直线
求椭圆的标准方程;第二问,分两种情况:当直线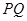 与
与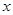 轴垂直时,比较直观,可求得
轴垂直时,比较直观,可求得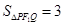 ,而当直线
,而当直线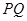 不与
不与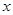 轴垂直时,设出直线
轴垂直时,设出直线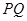 的方程,让它与椭圆联立,消去参数
的方程,让它与椭圆联立,消去参数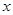 ,得到两根之和、两根之积,代入到
,得到两根之和、两根之积,代入到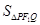 中,通过配方法求面积的最大值,利用内切圆半径
中,通过配方法求面积的最大值,利用内切圆半径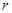 列出
列出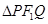 的面积,解出
的面积,解出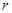 的范围,得到
的范围,得到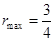 ,此时直线
,此时直线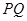 与
与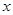 轴垂直,所以
轴垂直,所以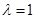 .
.
试题解析:(1)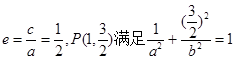 ,又
,又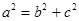
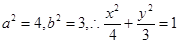 4分
4分
(2)显然直线 不与
不与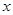 轴重合
轴重合
当直线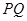 与
与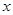 轴垂直时,|
轴垂直时,|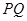 |=3,
|=3,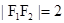 ,
,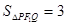 ; 5分
; 5分
当直线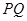 不与
不与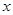 轴垂直时,设直线
轴垂直时,设直线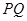 :
: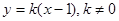 代入椭圆C的标准方程,
代入椭圆C的标准方程,
整理,得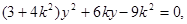
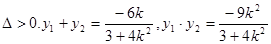 7分
7分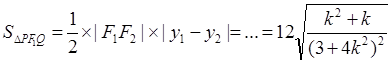
令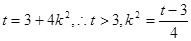
所以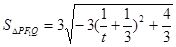
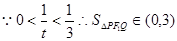
由上,得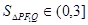
所以当直线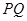 与
与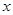 轴垂直时
轴垂直时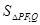 最大,且最大面积为3 10分
最大,且最大面积为3 10分
设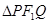 内切圆半径
内切圆半径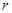 ,则
,则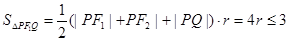
即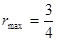 ,此时直线
,此时直线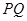 与
与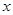 轴垂直,
轴垂直,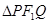 内切圆面积最大
内切圆面积最大
所以,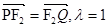 12分
12分
考点:1.椭圆的标准方程;2.直线的标准方程;3.韦达定理;4.三角形面积公式;5.配方法求最值.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
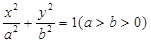 上的点
上的点 到左右两焦点
到左右两焦点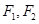 的距离之和为
的距离之和为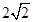 ,离心率为
,离心率为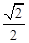 .
.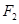 的直线
的直线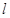 交椭圆于
交椭圆于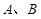 两点,若
两点,若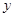 轴上一点
轴上一点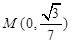 满足
满足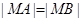 ,求直线
,求直线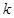 的值.
的值.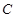 两焦点坐标分别为
两焦点坐标分别为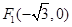 ,
,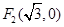 ,且经过点
,且经过点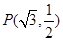 .
.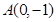 ,直线
,直线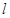 与椭圆
与椭圆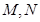 .若△
.若△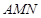 是以
是以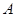 为直角顶点的等腰直角三角形,试求直线
为直角顶点的等腰直角三角形,试求直线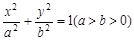 的左焦点,直线l:x=-
的左焦点,直线l:x=-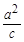 与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。
与x轴交于P点,MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|。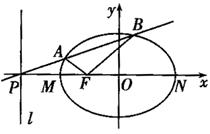
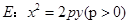 ,直线
,直线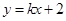 与E交于A、B两点,且
与E交于A、B两点,且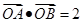 ,其中O为原点.
,其中O为原点.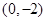 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为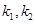 ,证明:
,证明: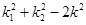 为定值.
为定值. 的两顶点坐标
的两顶点坐标 ,
,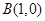 ,圆
,圆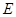 是
是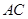 ,
,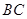 ,
, 上的切点分别为
上的切点分别为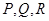 ,
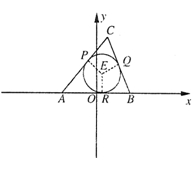
,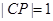 (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点 的轨迹为曲线
的轨迹为曲线 .
.
 ,当点
,当点 在以线段
在以线段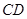 为直径的圆上时,求直线
为直径的圆上时,求直线 的离心率为
的离心率为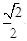 ,其中左焦点
,其中左焦点 (-2,0).
(-2,0).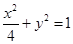 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.