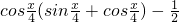题目内容
设函数y=f(x)满足:对任意的实数x∈R,有f(sinx)=-cos2x+cos2x+2sinx-3.(Ⅰ)求f(x)的解析式;
(Ⅱ)若方程
 有解,求实数a的取值范围.
有解,求实数a的取值范围.
【答案】分析:(Ⅰ)配凑法:f(sinx)=2sin2x-1+1-sin2x+2sinx-3=sin2x+2sinx-3,由此可得f(x);
(Ⅱ)先验证当 时方程
时方程 是否有解,再把方程化为2a=
是否有解,再把方程化为2a= ,此时只需求出
,此时只需求出 的值域即可,分类讨论:①当
的值域即可,分类讨论:①当 时,②当
时,②当 时,可求出其值域.
时,可求出其值域.
解答:解:(Ⅰ)f(sinx)=2sin2x-1+1-sin2x+2sinx-3=sin2x+2sinx-3,
所以f(x)=x2+2x-3(-1≤x≤1).
(Ⅱ)①当 时,
时, ,不成立.
,不成立.
②当 时,
时, ,
,
令 ,则
,则 ,
, ,
, ,
,
因为函数 在
在 上单增,所以
上单增,所以 .
.
③当 时,
时, ,
,
令 ,则
,则 ,
, ,
, ,
,
因为函数g(t)=t- +3在
+3在 上单增,所以2a≤g(
上单增,所以2a≤g( )=0⇒a≤0.
)=0⇒a≤0.
综上,实数a的取值范围是(-∞,0].
点评:本题考查函数解析式的求解及函数零点问题,考查学生分析问题解决问题的能力.
(Ⅱ)先验证当
 时方程
时方程 是否有解,再把方程化为2a=
是否有解,再把方程化为2a= ,此时只需求出
,此时只需求出 的值域即可,分类讨论:①当
的值域即可,分类讨论:①当 时,②当
时,②当 时,可求出其值域.
时,可求出其值域.解答:解:(Ⅰ)f(sinx)=2sin2x-1+1-sin2x+2sinx-3=sin2x+2sinx-3,
所以f(x)=x2+2x-3(-1≤x≤1).
(Ⅱ)①当
 时,
时, ,不成立.
,不成立.②当
 时,
时, ,
,令
 ,则
,则 ,
, ,
, ,
,因为函数
 在
在 上单增,所以
上单增,所以 .
.③当
 时,
时, ,
,令
 ,则
,则 ,
, ,
, ,
,因为函数g(t)=t-
 +3在
+3在 上单增,所以2a≤g(
上单增,所以2a≤g( )=0⇒a≤0.
)=0⇒a≤0.综上,实数a的取值范围是(-∞,0].
点评:本题考查函数解析式的求解及函数零点问题,考查学生分析问题解决问题的能力.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目