题目内容
将函数 的图象向右平移a(a>0)个单位,所得图象的函数为偶函数,则a的最小值为 ( )
的图象向右平移a(a>0)个单位,所得图象的函数为偶函数,则a的最小值为 ( )A.

B.

C.

D.

【答案】分析:先利用行列式的定义,化简函数,再利用两角和公式对函数解析式化简整理然后根据图象平移法则,得到平移后函数的解析式,利用诱导公式把正弦函数转化成余弦函数,然后根据偶函数关于y轴对称的性质求得a的最小值.
解答:解:由题意,函数 =
=
=2( cosx-
cosx- sinx)
sinx)
=2sin( -x)
-x)
=-2sin(x- )
)
图象向左平移a个单位,
所得函数图象是y1=-2sin(x+a- )
)
=-2cos[ -(x+a-
-(x+a- )]
)]
=-2cos(-x-a+ )
)
=2cos(x+a- )
)
是偶函数则关于y轴对称,
则a的最小值为a=
故选D
点评:本题以行列式为载体,考查行列式的定义,考查了函数奇偶性的性质.解题的关键是利用偶函数关于y轴对称的性质.
解答:解:由题意,函数
 =
=
=2(
 cosx-
cosx- sinx)
sinx)=2sin(
 -x)
-x)=-2sin(x-
 )
)图象向左平移a个单位,
所得函数图象是y1=-2sin(x+a-
 )
)=-2cos[
 -(x+a-
-(x+a- )]
)]=-2cos(-x-a+
 )
)=2cos(x+a-
 )
)是偶函数则关于y轴对称,
则a的最小值为a=

故选D
点评:本题以行列式为载体,考查行列式的定义,考查了函数奇偶性的性质.解题的关键是利用偶函数关于y轴对称的性质.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (其中
(其中 )图象的相邻两条对称轴间的距离为
)图象的相邻两条对称轴间的距离为 ,且图象上一个最高点的坐标为
,且图象上一个最高点的坐标为 .
. 的解析式;
的解析式; 的图象向右平移
的图象向右平移 个单位后,得到函数
个单位后,得到函数 的图象,求函数
的图象,求函数 的单调递减区间.
的单调递减区间. 的图象向右平移ϕ个单位,再将图象上每一点的横坐标缩短到原来的
的图象向右平移ϕ个单位,再将图象上每一点的横坐标缩短到原来的 倍,所得图象关于直线
倍,所得图象关于直线 对称,则ϕ的最小正值为( )
对称,则ϕ的最小正值为( )
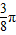

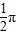
 的图象向右平移
的图象向右平移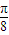 个单位得到函数y=g(x)的图象,则函数y=g(x)的解析式为 .
个单位得到函数y=g(x)的图象,则函数y=g(x)的解析式为 .