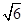题目内容
(本小题满分14分)
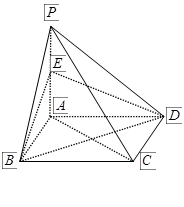
如图,四棱锥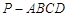 的底面
的底面 是边长为
是边长为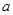 的正方形,
的正方形,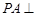 平面
平面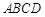 ,点
,点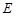 是
是 的中点.
的中点.
⑴求证: 平面
平面 ;
;
⑵求证:平面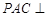 平面
平面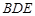 ;
;
⑶若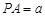 ,求三棱锥
,求三棱锥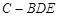 的体积.
的体积.
如图,四棱锥
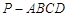 的底面
的底面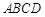 是边长为
是边长为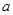 的正方形,
的正方形,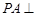 平面
平面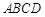 ,点
,点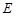 是
是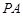 的中点.
的中点.
⑴求证:
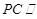 平面
平面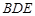 ;
;⑵求证:平面
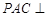 平面
平面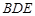 ;
;⑶若
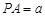 ,求三棱锥
,求三棱锥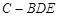 的体积.
的体积.⑴见解析; ⑵见解析;⑶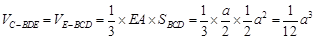 .
.
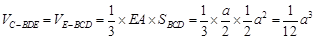 .
.本试题主要是考查了立体几何中线面的平行的证明以及面面垂直的郑敏而后三棱锥体积的运算的综合运用。
⑴要证明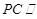 平面
平面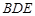 ;只要证明线线平行即可,运用判定定理得得到结论。
;只要证明线线平行即可,运用判定定理得得到结论。
⑵要证平面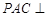 平面
平面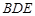 ;先通过线面垂直的证明,结合面面垂直的判定定理得到面面垂直。
;先通过线面垂直的证明,结合面面垂直的判定定理得到面面垂直。
⑶因为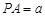 ,那么三棱锥
,那么三棱锥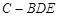 的体积利用转换顶点法来表示可得.
的体积利用转换顶点法来表示可得.
⑴设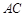 交
交 于
于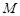 ,连结
,连结 .
.

因为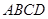 为正方形,所以
为正方形,所以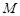 为
为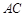 中点,又因为
中点,又因为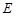 为
为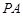 的中点,所以
的中点,所以 为
为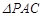 的中位线,
的中位线,
所以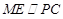 , ……………3分
, ……………3分
又因为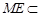 平面
平面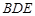 ,
,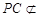 平面
平面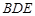 ,
,
所以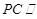 平面
平面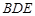 .……5分
.……5分
⑵因为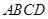 为正方形,所以
为正方形,所以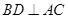 ,
,
因为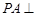 平面
平面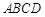 ,
,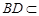 平面
平面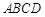 ,
,
所以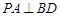 ,又
,又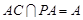 ,
,
所以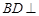 平面
平面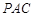 .………………………………………………………………8分
.………………………………………………………………8分
因为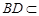 平面
平面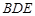 ,所以平面
,所以平面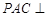 平面
平面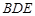 .…………………………10分
.…………………………10分
⑶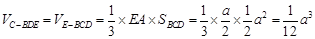 .…………………………14分
.…………………………14分
⑴要证明
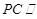 平面
平面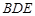 ;只要证明线线平行即可,运用判定定理得得到结论。
;只要证明线线平行即可,运用判定定理得得到结论。⑵要证平面
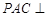 平面
平面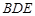 ;先通过线面垂直的证明,结合面面垂直的判定定理得到面面垂直。
;先通过线面垂直的证明,结合面面垂直的判定定理得到面面垂直。⑶因为
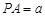 ,那么三棱锥
,那么三棱锥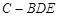 的体积利用转换顶点法来表示可得.
的体积利用转换顶点法来表示可得.⑴设
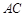 交
交 于
于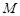 ,连结
,连结 .
.
因为
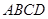 为正方形,所以
为正方形,所以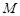 为
为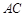 中点,又因为
中点,又因为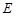 为
为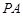 的中点,所以
的中点,所以 为
为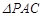 的中位线,
的中位线,所以
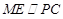 , ……………3分
, ……………3分又因为
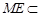 平面
平面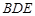 ,
,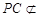 平面
平面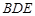 ,
,所以
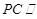 平面
平面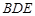 .……5分
.……5分 ⑵因为
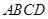 为正方形,所以
为正方形,所以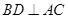 ,
, 因为
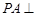 平面
平面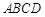 ,
,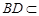 平面
平面 ,
,所以
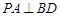 ,又
,又 ,
,所以
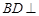 平面
平面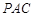 .………………………………………………………………8分
.………………………………………………………………8分因为
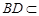 平面
平面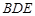 ,所以平面
,所以平面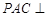 平面
平面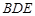 .…………………………10分
.…………………………10分⑶
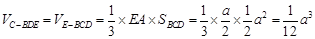 .…………………………14分
.…………………………14分
练习册系列答案
相关题目
 的棱长为
的棱长为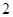 ,
,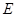 为
为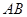 的中点.
的中点.
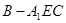 的体积;
的体积;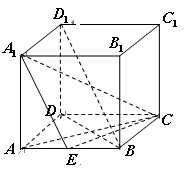
 是球
是球 表面上的点,
表面上的点,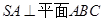 ,
,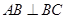 ,
,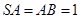 ,
,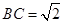 ,
,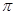
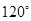 时,过圆锥顶点的截面中,最大截面面积为( )
时,过圆锥顶点的截面中,最大截面面积为( )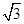
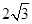

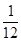
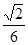

 ,类比以上结论,则长、宽、高分别为
,类比以上结论,则长、宽、高分别为 的长方体的外接球半径为( )
的长方体的外接球半径为( )



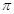 ,则该长方体的表面积的最大值为
,则该长方体的表面积的最大值为