题目内容
【题目】已知函数
.
（1）若
有三个极值点
，求
的取值范围；
（2）若
对任意
都恒成立的
的最大值为
，证明： 
.
【答案】(1) 
的取值范围为
；(2)见解析.
【解析】试题分析：（1）若
有三个极值点
，只需
应有两个既不等于0也不等于
的根；（2）
恒成立即
.变量分离，转化为函数最值问题.
（1）
，定义域为
，
，∵
，
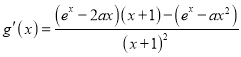
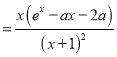只需
应有两个既不等于0也不等于
的根， 
，
①当
时， 
，∴
单增， 
最多只有一个实根，不满足；
②当
时， 
，
当
时， 
， 
单减；当
时， 
， 
单增；
∴
是
的极小值，
而
时， 
， 
时， 
，
要
有两根，只需
，由
，又由
，
反之，若
且
时，则
， 
的两根中，一个大于
，另一个小于
.
在定义域中，连同
， 
共有三个相异实根，且在三根的左右， 
正负异号，它们是
的三个极值点.
综上， 
的取值范围为
.
（2）
对
恒成立，
①当
或1时， 
均满足；
②
对
恒成立
对
恒成立，
记
， 
， 
， 
，
欲证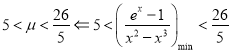
，
而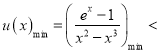
，
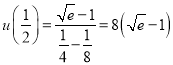只需证明
，显然成立.
下证：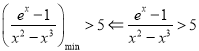 
， 
， 
， 
，
先证： 
， 
，
， 
.
令
， 
，
， 
， 
，∴
在
上单增，
∴
，∴
在
上单增，∴
，∴
在
上单增，
∴
，即证.
要证： 
， 
.
只需证
， 
， 
而
，开口向上，上不等式恒成立，从而得证命题成立.
练习册系列答案
相关题目
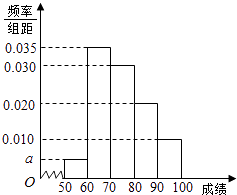
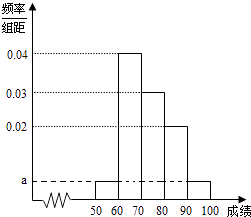
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（Ⅲ）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
