题目内容
(14分)已知等比数列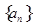 的前
的前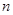 项和为
项和为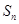 ,且
,且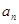 是
是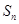 与2的等差中项,
与2的等差中项,
等差数列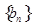 中,
中,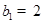 ,点
,点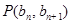 在直线
在直线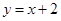 上.
上.
⑴求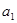 和
和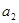 的值;
的值;
⑵求数列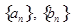 的通项
的通项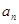 和
和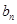 ;
;
⑶ 设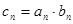 ,求数列
,求数列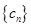 的前n项和
的前n项和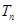 .
.
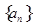 的前
的前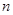 项和为
项和为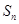 ,且
,且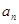 是
是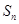 与2的等差中项,
与2的等差中项,等差数列
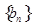 中,
中,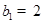 ,点
,点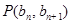 在直线
在直线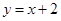 上.
上.⑴求
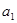 和
和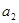 的值;
的值;⑵求数列
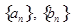 的通项
的通项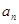 和
和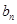 ;
;⑶ 设
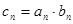 ,求数列
,求数列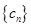 的前n项和
的前n项和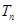 .
.(1)a2="4" ; (2bn=2n-1; (3)Tn=(2n-3)2n+1+6
本试题主要是考查了等差数列的通项公式的求解哦数列求和的综合运用。
(1) an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
进而得到第二项的值。对于又Sn—Sn-1=an,
∴an=2an-2an-1∴ ,即数列{an}是等比数据列
,即数列{an}是等比数据列
以及∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0得到数列的通项公式。
(2)由上可知,cn=(2n-1)2n
利用错位相减法可知得到数列的和的求解。
解:(1)∵an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
a1+a2=S2=2a2-2,解得a2=4 ……3分
(2)∵Sn=2an-2,Sn-1=2an-1-2,
又Sn—Sn-1=an,
∴an=2an-2an-1,
∵an≠0,
∴ ,即数列{an}是等比树立∵a1=2,∴an=2n
,即数列{an}是等比树立∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1, ……8分
(3)∵cn=(2n-1)2n
∴Tn=a1b1+ a2b2+····anbn=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
因此:-Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn=(2n-3)2n+1+6 ……14分
(1) an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
进而得到第二项的值。对于又Sn—Sn-1=an,

∴an=2an-2an-1∴
 ,即数列{an}是等比数据列
,即数列{an}是等比数据列以及∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0得到数列的通项公式。
(2)由上可知,cn=(2n-1)2n
利用错位相减法可知得到数列的和的求解。
解:(1)∵an是Sn与2的等差中项
∴Sn=2an-2 ∴a1=S1=2a1-2,解得a1=2
a1+a2=S2=2a2-2,解得a2=4 ……3分
(2)∵Sn=2an-2,Sn-1=2an-1-2,
又Sn—Sn-1=an,

∴an=2an-2an-1,
∵an≠0,
∴
 ,即数列{an}是等比树立∵a1=2,∴an=2n
,即数列{an}是等比树立∵a1=2,∴an=2n∵点P(bn,bn+1)在直线x-y+2=0上,∴bn-bn+1+2=0,
∴bn+1-bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n-1, ……8分
(3)∵cn=(2n-1)2n
∴Tn=a1b1+ a2b2+····anbn=1×2+3×22+5×23+····+(2n-1)2n,
∴2Tn=1×22+3×23+····+(2n-3)2n+(2n-1)2n+1
因此:-Tn=1×2+(2×22+2×23+···+2×2n)-(2n-1)2n+1,
即:-Tn=1×2+(23+24+····+2n+1)-(2n-1)2n+1,
∴Tn=(2n-3)2n+1+6 ……14分

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
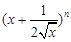 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列. (n∈N*),求{bn}的前n项和公式Tn.
(n∈N*),求{bn}的前n项和公式Tn.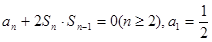
 }是等差数列;
}是等差数列; 有n条弦的长度成等差数列,最小弦长为数列的
有n条弦的长度成等差数列,最小弦长为数列的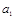 ,最大弦长为
,最大弦长为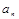 ,若公差
,若公差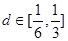 ,那么n的取值集合为( )
,那么n的取值集合为( ) 中,
中,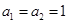 ,且
,且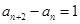 ,则数列
,则数列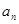 }的前
}的前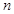 项和为
项和为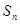 ,且
,且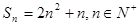 ,数列{
,数列{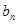 }满足
}满足 。
。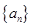 、{
、{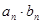 }的前
}的前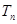 。
。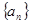 为等比数列,
为等比数列,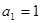 ,
,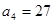 ,
,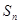 为等差数列
为等差数列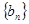 的前
的前 项和,
项和,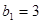 ,
,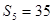 。
。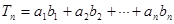 ,求
,求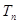 。
。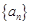 为等差数列,
为等差数列,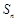 是其前n项的和,且
是其前n项的和,且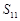 =
=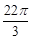 ,则
,则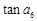 的值为
的值为