题目内容
相关变量x、y的样本数据如下表：
经回归分析可得y与x线性相关，并由最小二乘法求得回归直线方程为
=1.1x+a，则a=（ ）
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 2 | 3 | 5 | 6 |
| ? |
| y |
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
分析：由样本数据可得，
=3，
=3.6，代入可求这组样本数据的回归直线方程．
. |
| x |
. |
| y |
解答：解：由题意，
=
=3，
=
=3.6，
∵回归直线方程为
=1.1x+a，
∴3.6=1.1×3+a，
∴a=0.3．
故选：C．
. |
| x |
| 1+2+3+4+5 |
| 5 |
. |
| y |
| 2+2+3+5+6 |
| 5 |
∵回归直线方程为
| ? |
| y |
∴3.6=1.1×3+a，
∴a=0.3．
故选：C．
点评：本题考查数据的回归直线方程，利用回归直线方程恒过样本中心点是关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
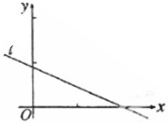设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（ ）| A、x和y的相关系数为直线l的斜率 | ||||
| B、x和y的相关系数在0到1之间 | ||||
| C、当n为偶数时，分布在l两侧的样本点的个数一定相同 | ||||
D、直线l过点（
|
设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n次方个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论正确的是（ ）A、直线l过点(
| ||||
| B、x和y的相关系数为直线l的斜率 | ||||
| C、x和y的相关系数在0到1之间 | ||||
| D、当n为偶数时，分布在l两侧的样本点的个数一定相同 |
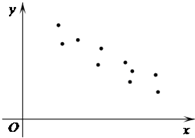设（x1，y1），（x2，y2），…，（xn，yn），是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归方程（如图），以下结论中正确的是（ ）| A、x和y正相关 | B、x和y的相关系数为直线l的斜率 | C、x和y的相关系数在-1到0之间 | D、当n为偶数时，分布在l两侧的样本点的个数一定相同 |