题目内容
已知k<1,求不等式
>1的解集.
| k(x-1) |
| x-2 |
当x-2>0即x>2时,原不等式去分母得:kx-k>x-2,
即(k-1)x>k-2,又k<1,即k-1<0,
解得:x<
=1+
<1,则原不等式无解;
当x-2<0即x<2时,原不等式去分母得:kx-k<x-2,
即(k-1)x<k-2,又k<1,即k-1<0,
解得:x>
,原不等式的解集为:
<x<2,
综上,原不等式的解集为(
,2).
即(k-1)x>k-2,又k<1,即k-1<0,
解得:x<
| k-2 |
| k-1 |
| 1 |
| k-1 |
当x-2<0即x<2时,原不等式去分母得:kx-k<x-2,
即(k-1)x<k-2,又k<1,即k-1<0,
解得:x>
| k-2 |
| k-1 |
| k-2 |
| k-1 |
综上,原不等式的解集为(
| k-2 |
| k-1 |

练习册系列答案
相关题目
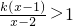 的解集.
的解集.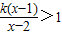 的解集.
的解集.