题目内容
(Ⅰ)已知函数f(x)=lnx-x+1,x∈(0,+∞),求函数f(x)的最大值;
(Ⅱ)设a1,b1(k=1,2…,n)均为正数,证明:
(1)若a1b1+a2b2+…anbn≤b1+b2+…bn,则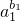
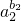 …
…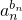 ≤1;
≤1;
(2)若b1+b2+…bn=1,则 ≤
≤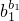
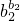 …
…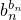 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.
解:(I)f(x)的定义域为(0,+∞),
令f′(x)= -1=0,解得x=1,
-1=0,解得x=1,
当0<x<1时,f′(x)>0,所以f(x)在(0,1)上是增函数;
当x>1时,f′(x)<0,所以f(x)在(1,+∞)上是减函数;
故函数f(x)在x=1处取得最大值f(1)=0;
(II)(1)由(I)知,当x∈(0,+∞)时,有f(x)≤f(1)=0,即lnx≤x-1,
∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak-1,
得bklnak≤akbk-bk(k=1,2…,n),
求和得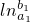

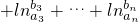 ≤a1b1+a2b2+…+anbn-(b1+b2+…+bn)
≤a1b1+a2b2+…+anbn-(b1+b2+…+bn)
∵a1b1+a2b2+…anbn≤b1+b2+…bn,
∴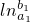

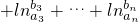 ≤0,即ln
≤0,即ln ≤0,
≤0,
∴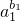
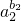 …
…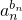 ≤1;
≤1;
(2)先证 ≤
≤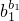
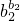 …
…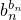 ,
,
令ak=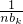 (k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,
(k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,
于是由(1)得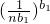
 ≤1,即
≤1,即 ≤nb1+b2+…bn=n,
≤nb1+b2+…bn=n,
∴ ≤
≤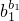
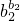 …
…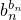 ,
,
②再证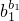
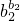 …
…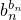 ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,
记s=b12+b22+…+bn2.令ak= (k=1,2…,n),
(k=1,2…,n),
则a1b1+a2b2+…+anbn= (b12+b22+…+bn2)=1=b1+b2+…bn,
(b12+b22+…+bn2)=1=b1+b2+…bn,
于是由(1)得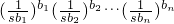 ≤1,
≤1,
即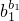
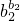 …
…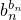 ≤sb1+b2+…bn=s,
≤sb1+b2+…bn=s,
∴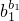
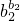 …
…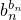 ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,
综合①②,(2)得证.
分析:(Ⅰ)求导,令导数等于零,解方程,分析该零点两侧导函数的符号,确定函数的单调性和极值,最终求得函数的最值;
(Ⅱ)(1)要证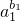
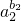 …
…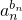 ≤1,只需证ln
≤1,只需证ln ≤0,根据(I)和∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak-1,即可证明结论;(2)要证
≤0,根据(I)和∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak-1,即可证明结论;(2)要证 ≤
≤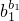
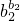 …
…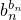 ,根据(1),令ak=
,根据(1),令ak=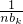 (k=1,2…,n),再利用分数指数幂的运算法则即可证得结论;要证
(k=1,2…,n),再利用分数指数幂的运算法则即可证得结论;要证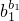
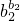 …
…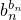 ≤b12+b22+…+bn2,记s=b12+b22+…+bn2.令ak=
≤b12+b22+…+bn2,记s=b12+b22+…+bn2.令ak= (k=1,2…,n),同理可证.
(k=1,2…,n),同理可证.
点评:此题是个难题.本题主要考查函数、导数、不等式证明等基础知识,同时考查综合运用数学知识进行推理论证的能力,以及化归与转化的思想.
令f′(x)=
 -1=0,解得x=1,
-1=0,解得x=1,当0<x<1时,f′(x)>0,所以f(x)在(0,1)上是增函数;
当x>1时,f′(x)<0,所以f(x)在(1,+∞)上是减函数;
故函数f(x)在x=1处取得最大值f(1)=0;
(II)(1)由(I)知,当x∈(0,+∞)时,有f(x)≤f(1)=0,即lnx≤x-1,
∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak-1,
得bklnak≤akbk-bk(k=1,2…,n),
求和得
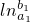

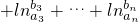 ≤a1b1+a2b2+…+anbn-(b1+b2+…+bn)
≤a1b1+a2b2+…+anbn-(b1+b2+…+bn)∵a1b1+a2b2+…anbn≤b1+b2+…bn,
∴
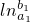

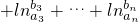 ≤0,即ln
≤0,即ln ≤0,
≤0,∴
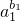
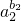 …
…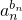 ≤1;
≤1;(2)先证
 ≤
≤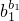
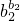 …
…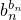 ,
,令ak=
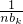 (k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,
(k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,于是由(1)得
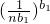
 ≤1,即
≤1,即 ≤nb1+b2+…bn=n,
≤nb1+b2+…bn=n,∴
 ≤
≤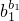
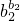 …
…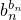 ,
,②再证
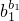
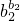 …
…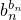 ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,记s=b12+b22+…+bn2.令ak=
 (k=1,2…,n),
(k=1,2…,n),则a1b1+a2b2+…+anbn=
 (b12+b22+…+bn2)=1=b1+b2+…bn,
(b12+b22+…+bn2)=1=b1+b2+…bn,于是由(1)得
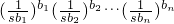 ≤1,
≤1,即
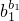
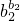 …
…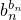 ≤sb1+b2+…bn=s,
≤sb1+b2+…bn=s,∴
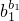
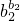 …
…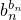 ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,综合①②,(2)得证.
分析:(Ⅰ)求导,令导数等于零,解方程,分析该零点两侧导函数的符号,确定函数的单调性和极值,最终求得函数的最值;
(Ⅱ)(1)要证
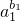
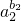 …
…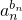 ≤1,只需证ln
≤1,只需证ln ≤0,根据(I)和∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak-1,即可证明结论;(2)要证
≤0,根据(I)和∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak-1,即可证明结论;(2)要证 ≤
≤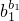
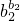 …
…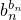 ,根据(1),令ak=
,根据(1),令ak=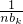 (k=1,2…,n),再利用分数指数幂的运算法则即可证得结论;要证
(k=1,2…,n),再利用分数指数幂的运算法则即可证得结论;要证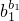
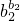 …
…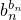 ≤b12+b22+…+bn2,记s=b12+b22+…+bn2.令ak=
≤b12+b22+…+bn2,记s=b12+b22+…+bn2.令ak= (k=1,2…,n),同理可证.
(k=1,2…,n),同理可证.点评:此题是个难题.本题主要考查函数、导数、不等式证明等基础知识,同时考查综合运用数学知识进行推理论证的能力,以及化归与转化的思想.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|