Question

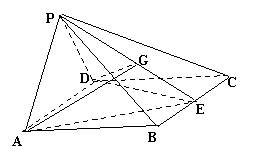 (本小题满分12分)、四棱锥P—ABCD中，侧面PAD底面ABCD，底面ABCD是边长为2的正方形，又PA=PD，，E、G分别是BC、PE的中点。

（1）求证：ADPE；

   （2）求二面角E—AD—G的正切值。

Answer 1

解：解法一：

   （1）如图，取AD的中点O，连结OP，OE

 （ 2分）

       又E是BC的中点，

       ∴  （4分）

       又OP∩OE=0，∴平面OPE。

而平面OPE， ∴      （ 6分）

（2）取OE的中点F，连结FG，OG，则由（1）易知ADOG，又OEAD，

       ∴就是二面角E—AD—G的平面角  （ 9分）

  ∵PA=PD，，∴△APD为等边三角形，且边长为2

∴OP=，       ∴ 

 ∴   （12分）

       解法二：（1）同解法一。

（2）建立如图所示的空间直角坐标系，

则A（1，0，0），D（―1，0，0），P（0，0，），E（0，2，0）

       ∴  （8分）

       设平面ADG的法向量为

       由，      得

       ∴   10分

       又平面EAD的一个法向量为

       又因为       （11分）

       ∴二面角E—AD—G的余弦值为   （ 12分）