题目内容
已知函数f（x）=ax+x-3与函数g（x）=x+logax-3的零点分别为x1和x2
- A.x1-
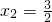
- B.x1-x2=3
- C.x1+
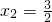
- D.x1+x2=3
D
分析：构建函数F（x）=ax，G（x）=logax，h（x）=3-x，不妨设a＞1，在同一坐标系中作出三个函数的图象，求出y=x与y=3-x交点的横坐标为
，即可求得x1+x2的值．
解答：
解：由题意，构建函数F（x）=ax，G（x）=logax，h（x）=3-x
不妨设a＞1，在同一坐标系中作出三个函数的图象，
注意到F（x）=ax，G（x）=logax，关于直线y=x对称
可以知道A，B关于y=x对称
由于y=x与y=3-x交点的横坐标为
所以x1+x2=3
故选D．
点评：函数的零点研究，我们利用数形结合的方法，指数函数与对数函数互为反函数，我们应注意图象关于直线y=x对称．
分析：构建函数F（x）=ax，G（x）=logax，h（x）=3-x，不妨设a＞1，在同一坐标系中作出三个函数的图象，求出y=x与y=3-x交点的横坐标为
，即可求得x1+x2的值．解答：
解：由题意，构建函数F（x）=ax，G（x）=logax，h（x）=3-x不妨设a＞1，在同一坐标系中作出三个函数的图象，
注意到F（x）=ax，G（x）=logax，关于直线y=x对称
可以知道A，B关于y=x对称
由于y=x与y=3-x交点的横坐标为
所以x1+x2=3
故选D．
点评：函数的零点研究，我们利用数形结合的方法，指数函数与对数函数互为反函数，我们应注意图象关于直线y=x对称．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目