题目内容
【题目】已知函数
（常数
）.
（1）讨论
的单调性；
（2）设
是的导函数，求证：
.
【答案】（1）见解析;（2）见解析.
【解析】试题分析：（1）先求导数，再求导函数零点，根据两零点大小分类讨论，确定导函数符号变化规律，进而确定单调性，（2）先化简所证不等式，再利用导函数证
（
），即得
（），最后再利用导数证
（差函数或商函数），根据
等号不同时成立得结论.
试题解析：（1）
（，
）
画出
（）及
（）的图象，它们的零点分别为
和
①当
时，
在
，
，
②当
时，在
③当
时，在
，
，
（2）因
要证
，需证
（）
法1.即证
（）
设
（），
（）
一方面
（）
在
，
则
①
另一方面，
（）
在
，
则
②
据①②
有因①的取等条件是
，②的取等条件是
故
，即（），即
法2先证（）（差函数）
进而（）
再证（差函数或商函数）
说明等号不成立
故（）成立.
练习册系列答案
阅读快车系列答案
相关题目
【题目】一只红铃虫的产卵数y和温度x有关，现收集了6组观测数据于下表中，通过散点图可以看出样本点分布在一条指数型函数y=
的图象的周围.
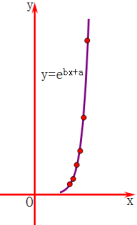
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数)；
(2)试用(1)中的回归曲线方程求相应于点(24，17)的残差
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明：
①结果中的
都应按题目要求保留两位小数.但在求
时请将
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式：回归直线方程的斜率=
=
，截距
.
③下面的参考数据可以直接引用：
=25，
=31.5，
≈3.05，
=5248，
≈476.08，
，ln18.17≈2.90.
