题目内容
【题目】在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集![]() 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“![]() ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量![]() ,“
,“![]() ”当且仅当“
”当且仅当“![]() ”或“
”或“![]() ”。按上述定义的关系“
”。按上述定义的关系“![]() ”,给出如下四个命题:
”,给出如下四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则对于任意
,则对于任意![]() ;
;
④对于任意向量![]() ,若
,若![]() ,则
,则![]() 。
。
其中真命题的序号为__________
【答案】①②③
【解析】
试题①因为![]() ,所以,
,所以,![]() ,
,![]() ,
,![]() ,所以有:
,所以有:![]() ,①为真命题;
,①为真命题;
②设:![]() ,
,
由![]() 得“
得“![]() ”或“
”或“![]() ”
”
由![]() 得“
得“![]() ”或“
”或“![]() ”
”
若![]() ,则定义可知
,则定义可知![]()
若![]() 且“
且“![]() ”,则
”,则![]() ,所以,
,所以,![]()
若![]() 且
且![]() ,则
,则![]() 所以,
所以,![]()
若“![]() ”且“
”且“![]() ”则,
”则,![]() ,所以,
,所以,![]()
综上所述:若![]() ,则
,则![]() 正确;
正确;
③设:![]() ,则
,则![]()
由![]() 得:“
得:“![]() ”或“
”或“![]() ”
”
若“![]() ”,则
”,则![]() ,所以,
,所以,![]()
若![]() ,则
,则![]() 且
且![]() ,从而有
,从而有![]()
综上所述,若![]() ,则对于任意
,则对于任意![]() ;命题③正确;
;命题③正确;
④设:![]() ,
,
由![]() 得“
得“![]() ”或“
”或“![]() ”
”
由![]() 得:“
得:“![]() ”或“
”或“![]() ”
”
若![]() 且“
且“![]() ”,同时,
”,同时,![]() 则“
则“![]() ”,所以
”,所以![]() 不成立
不成立
所以,④不正确;
综上可知,只有①②③正确,所以答案应填:①②③.

练习册系列答案
相关题目
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取100名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在![]() 的男生人数有16人.
的男生人数有16人.
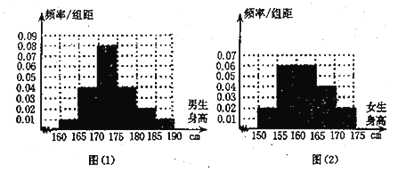
(1)试问在抽取的学生中,男,女生各有多少人?
(2)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分之几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(3)在上述100名学生中,从身高在![]() 之间的男生和身高在
之间的男生和身高在![]() 之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
之间的女生中间按男、女性别分层抽样的方法,抽出6人,从这6人中选派2人当旗手,求2人中恰好有一名女生的概率.
参考公式:![]()
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
5.024 | 6.635 | 7.879 | 10.828 |