题目内容
 张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为
张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数X的数学期望.
分析:(Ⅰ)设走L1路线最多遇到1次红灯为A事件,利用排列组合知识能求出走L1路线,最多遇到1次红灯的概率.
(Ⅱ)依题意,X的可能取值为0,1,2.分别求出其概率,由此能求出随机变量X的分布列和数学期望.
(Ⅱ)依题意,X的可能取值为0,1,2.分别求出其概率,由此能求出随机变量X的分布列和数学期望.
解答:解:(Ⅰ)设走L1路线最多遇到1次红灯为A事件,
则P(A)=
×(
)3+
×
×(
)2=
.…(5分)
所以走L1路线,最多遇到1次红灯的概率为
.
(Ⅱ)依题意,X的可能取值为0,1,2.…(6分)
P(X=0)=(1-
)×(1-
)=
,
P(X=1)=
×(1-
)+(1-
)×
=
,
P(X=2)=
×
=
.…(9分)
∴随机变量X的分布列为:
EX=
×0+
×1+
×2=
. …(12分)
则P(A)=
| C | 0 3 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以走L1路线,最多遇到1次红灯的概率为
| 1 |
| 2 |
(Ⅱ)依题意,X的可能取值为0,1,2.…(6分)
P(X=0)=(1-
| 3 |
| 4 |
| 3 |
| 5 |
| 1 |
| 10 |
P(X=1)=
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
P(X=2)=
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 10 |
| 9 |
| 20 |
| 9 |
| 20 |
| 27 |
| 20 |
点评:本题考查离散型随机变量的分布列和数学期望,是历年高考的必考题型.解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
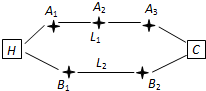 (2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为
(2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
. 的数学期望;
的数学期望;
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
. 的数学期望;
的数学期望;
 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
 的数学期望;
的数学期望;