题目内容
17.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}+2\overrightarrow{b}$|=( )| A. | 2 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 由已知条件及向量数量积的运算即可求出$(\overrightarrow{a}+2\overrightarrow{b})^{2}=12$,从而便求出$|\overrightarrow{a}+2\overrightarrow{b}|$.
解答 解:根据已知条件,$(\overrightarrow{a}+2\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$=4+4+4=12;
∴$|\overrightarrow{a}+2\overrightarrow{b}|=2\sqrt{3}$.
故选:D.
点评 考查数量积的运算及数量积的计算公式,求向量$\overrightarrow{a}+2\overrightarrow{b}$的长度先求$(\overrightarrow{a}+2\overrightarrow{b})^{2}$的方法.

练习册系列答案
相关题目
1.已知x,y∈R,i为虚数单位,若$\frac{x}{1+i}$=1-yi,则x+yi=( )
| A. | 2+i | B. | 1+2i | C. | 1-2i | D. | 2-i |
5.阅读如图所示的框图,运行相应的程序,则输出S的值为( )
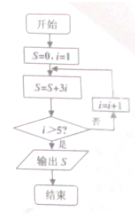

| A. | 30 | B. | 45 | C. | 63 | D. | 84 |
 如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点
如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点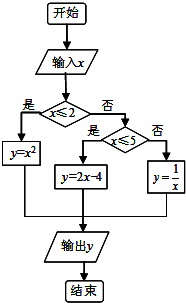 如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3.
如图给出了一个程序框图,其作用是输入x的值输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值的个数是3.