题目内容
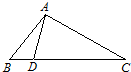
如图，△ABC中，∠C=90°，⊙O分别切AC、BC于M、N，圆心O在AB上，⊙O的半径为12cm，BO=20cm，则AO的长为分析：做出辅助线，根据切线的性质定理，得到四边形是一个正方形，根据所给的线段的长度，用勾股定理得到BN长度，根据平行线分线段成比例定理得到比例式，把已知的线段代入得到结果．
解答：
解：如图，连接ON、OM，则∠ONC=∠OMC=90°，因此四边形ONCM为正方形，
∴CN=CM=ON=12cm，在Rt△OBN中，BN=
∵ON∥AC
∴
=
∴AO=
=
=15cm．
故答案为：15cm
解：如图，连接ON、OM，则∠ONC=∠OMC=90°，因此四边形ONCM为正方形，∴CN=CM=ON=12cm，在Rt△OBN中，BN=
| BO2-ON2 |
∵ON∥AC
∴
| BN |
| NC |
| BO |
| AO |
∴AO=
| NC•BO |
| BN |
| 12×20 |
| 16 |
故答案为：15cm
点评：本题考查相似三角形的性质，本题解题的关键是根据比例式写出关于要求变量的方程解方程即可，本题是一个基础题．
练习册系列答案
相关题目
如图，
如图，△ABC中，
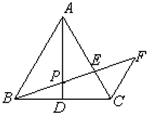如图，△ABC中，AB=AC，AD是中线，P为AD上一点，CF∥AB，BP延长线交AC、CF于E、F，
已知：如图，△ABC中，∠B=60°，AD，CE是角平分线．