题目内容
1.设函数f(x)=-|x|,g(x)=lg(ax2-4x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为(-∞,4].分析 求出f(x),g(x)的值域,则f(x)的值域为g(x)的值域的子集.
解答 解:f(x)=-|x|≤0,∴f(x)的值域是(-∞,0].
设g(x)的值域为A,
∵对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),
∴(-∞,0]⊆A.
设y=ax2-4x+1的值域为B,
则(0,1]⊆B.
显然当a=0时,上式成立.
当a>0时,△=16-4a≥0,解得0<a≤4.
当a<0时,ymax=$\frac{4a-16}{4a}$≥1,即1-$\frac{4}{a}$≥1恒成立.
综上可得:实数a的取值范围为:(-∞,4],
故答案为:(-∞,4]
点评 本题考查了函数的值域,集合的包含关系,二次函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.给出关于复数z=$\frac{2}{1+i}$的四个命题:p1:|z|=2;p2:z2=2i:p3:$\overline z=1+i$:p4.z的虚部为-1.下列命题中为真命题的是( )
| A. | p1∧p2 | B. | p1∨p2 | C. | (?P3)∧p4 | D. | (?p3)∨p4 |
12.与y=x为同一函数的是( )
| A. | y=($\sqrt{x}$)2 | B. | y=$\frac{{x}^{2}}{x}$ | C. | y=$\left\{\begin{array}{l}{x,(x>0)}\\{-x,(x<0)}\end{array}\right.$ | D. | y=$\root{3}{{x}^{3}}$ |
9.已知a1=1,${a_n}=n({a_{n+1}}-{a_n})(n∈{N^*})$,则数列{an}的通项公式是( )
| A. | n | B. | ${(\frac{n+1}{n})^{n-1}}$ | C. | n2 | D. | 2n-1 |
16.已知集合A={1,2,3},B={-2,-1,0,1,2},则A∩B=( )
| A. | {1,2,3} | B. | {-2,-1,0,1,2} | C. | {1,2} | D. | {-2,-1} |
13. 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
 如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为( )| A. | 4π | B. | 2π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
10.函数$f(x)=\frac{2}{x}$的单调递减区间为( )
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (0,+∞) |
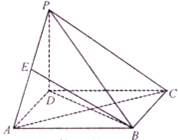 如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,
如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥底面ABCD,PD=AB,