题目内容
若a=∫2xdx，则在（3x2-
）5的二项展开式中，常数项为 ．
【答案】分析：由定积分的定义，令F'（x）=x，则F（x）
=x2，由公式求出积分值，从而求出a的值，再用展开式的通项求常数项．
解答：解：由导数的运算法则知当F（x）=
x2时，F'（x）=x
由定积分的定义得
a=∫2xdx=F（2）-F（0）=2-0=2
（3x2-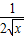
）5展开式的通项为T k+1=C5k（3x2）5-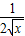k（-
）k=（-
）k35-kC5kx10-
k
令10-
k=0得k=4
展开式中的常数项为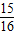
故答案为：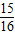
点评：本题考点是定积分，此类题高中要求较低，能根据公式求值即可，以及二项展开式的通项公式是解决二项展开式特殊项问题的方法．
=x2，由公式求出积分值，从而求出a的值，再用展开式的通项求常数项．解答：解：由导数的运算法则知当F（x）=
x2时，F'（x）=x由定积分的定义得
a=∫2xdx=F（2）-F（0）=2-0=2
（3x2-
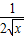）5展开式的通项为T k+1=C5k（3x2）5-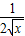k（-）k=（-）k35-kC5kx10-k令10-
k=0得k=4展开式中的常数项为
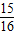
故答案为：
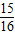
点评：本题考点是定积分，此类题高中要求较低，能根据公式求值即可，以及二项展开式的通项公式是解决二项展开式特殊项问题的方法．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
）5的二项展开式中，常数项为 ．
）5的二项展开式中，常数项为 ．