题目内容
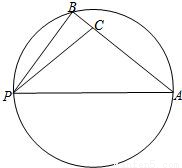
如图,点B在以PA为直径的圆周上,点C在线段AB上,已PA=5,PB=3,PC=
,设∠APB=α,∠APC=β,α,β均为锐角.
(1)求β;
(2)求向量
,
的数量积
•
的值.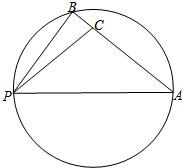
15
| ||
| 7 |
(1)求β;
(2)求向量
| AC |
| PC |
| AC |
| PC |

(1):因为点B在以PA为直径的圆周上,所以∠ABP=90°,
所以cosα=
=
,sinα=
.
所以tanα=
,
cos∠CPB=cos(α-β)=
=
=
,sin(α-β)=
,
所以tan(α-β)=
,
tanβ=tan[α-(α-β)]=
=1,
又β∈(0,
),所以β=
.
(2)
•
=(
-
)•
=
2-
•
=(
)2-5×
×
=-
故答案为β=
;
•
=-
所以cosα=
| PB |
| PA |
| 3 |
| 5 |
| 4 |
| 5 |
所以tanα=
| 4 |
| 3 |
cos∠CPB=cos(α-β)=
| PB |
| PC |
| 3 | ||||
|
7
| ||
| 10 |
| ||
| 10 |
所以tan(α-β)=
| 1 |
| 7 |
tanβ=tan[α-(α-β)]=
| tanα-tan(α-β) |
| 1+tanαtan(α-β) |
又β∈(0,
| π |
| 2 |
| π |
| 4 |
(2)
| AC |
| PC |
| PC |
| PA |
| PC |
| PC |
| PA |
| PC |
=(
15
| ||
| 7 |
15
| ||
| 7 |
| ||
| 2 |
| 75 |
| 49 |
故答案为β=
| π |
| 4 |
| AC |
| PC |
| 75 |
| 49 |

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
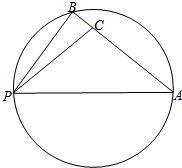 如图,点B在以PA为直径的圆周上,点C在线段AB上,已
如图,点B在以PA为直径的圆周上,点C在线段AB上,已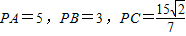 ,设∠APB=α,∠APC=β,α,β均为锐角.
,设∠APB=α,∠APC=β,α,β均为锐角.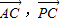 的数量积
的数量积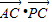 的值.
的值.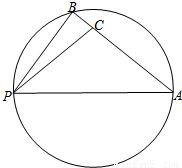
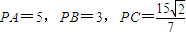 ,设∠APB=α,∠APC=β,α,β均为锐角.
,设∠APB=α,∠APC=β,α,β均为锐角.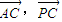 的数量积
的数量积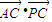 的值.
的值.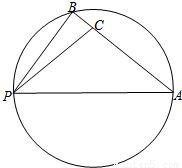
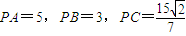 ,设∠APB=α,∠APC=β,α,β均为锐角.
,设∠APB=α,∠APC=β,α,β均为锐角.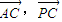 的数量积
的数量积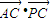 的值.
的值.