题目内容
在△ABC中,角A、B、C的对边分别为 、
、 、
、 ,若
,若 =
= ,则△ABC的形状为( )
,则△ABC的形状为( )
A、正三角形 B、直角三角形
C、等腰三角形或直角三角形 D、等腰直角三角形
 、
、 、
、 ,若
,若 =
= ,则△ABC的形状为( )
,则△ABC的形状为( )A、正三角形 B、直角三角形
C、等腰三角形或直角三角形 D、等腰直角三角形
B
分析:利用二倍角公式代入cos2
 =
=  求得cosB=
求得cosB=  ,进而利用余弦定理化简整理求得a2+b2=c2,根据勾股定理判断出三角形为直角三角形.
,进而利用余弦定理化简整理求得a2+b2=c2,根据勾股定理判断出三角形为直角三角形.解:∵cos2
 =
= ,∴
,∴ =
= ,∴cosB=
,∴cosB= ,
,∴
 =
= ,
,∴a2+c2-b2=2a2,即a2+b2=c2,
∴△ABC为直角三角形.
故选B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,BC=2,C=
,BC=2,C= ,则边AB的长度等于_____________.
,则边AB的长度等于_____________.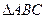 中,内角A,B,C的对边分别是
中,内角A,B,C的对边分别是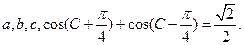
 求a,b.
求a,b. ,cosC是方程
,cosC是方程 的一个根,求△ABC周长的最小值。
的一个根,求△ABC周长的最小值。 中,
中, ,则角
,则角 等于( )
等于( ) 




 ,其中
,其中 (1)若
(1)若 。求函数
。求函数 的最小值及相应x的值;(2)若
的最小值及相应x的值;(2)若 的
的 ,且
,且 ,求
,求 的值。
的值。

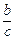 +
+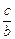 的取值范围是 .
的取值范围是 .