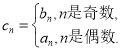题目内容
【题目】已知动点![]() 到直线
到直线![]() 的距离比到点
的距离比到点![]() 的距离大
的距离大![]()
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)![]() 为
为![]() 上两点,
上两点,![]() 为坐标原点,
为坐标原点,![]() ,过
,过![]() 分别作
分别作![]() 的两条切线,相交于点
的两条切线,相交于点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(1)轨迹![]() 为抛物线,其方程为
为抛物线,其方程为![]() .(2)
.(2)![]()
【解析】
(1)设点![]() 的坐标为
的坐标为![]() ,根据条件列出方程
,根据条件列出方程![]() ,然后化简即可;
,然后化简即可;
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立直线与抛物线的方程得出
,联立直线与抛物线的方程得出![]() ,然后用
,然后用![]() 表示出
表示出![]() 和点
和点![]() 到直线
到直线![]() 的距离
的距离![]() ,然后可得到
,然后可得到![]() ,即可求出其最小值.
,即可求出其最小值.
(1)设点![]() 的坐标为
的坐标为![]()
因为动点![]() 到定直线
到定直线![]() 的距离比到点
的距离比到点![]() 的距离大
的距离大![]()
所以![]() ,且
,且![]() ,化简得
,化简得![]()
所以轨迹![]() 为抛物线,其方程为
为抛物线,其方程为![]()
(2)依题意,设直线![]() 的方程为
的方程为![]()
由![]() ,得
,得![]()
因为直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点
所以![]()
设![]() ,
,
又因为![]()
所以![]()
所以![]()
所以![]()
所以![]()
所以![]()
![]()
由![]()
过点![]() 的切线方程为
的切线方程为![]() ,即
,即![]() ①
①
过点![]() 的切线方程为
的切线方程为![]() ,即
,即![]() ②
②
由①②得![]() ,
,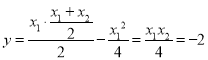 ,
,
所以过![]() 的两条抛物线的切线相交于点
的两条抛物线的切线相交于点![]()
所以点![]() 到直线
到直线![]() 的距离
的距离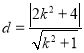
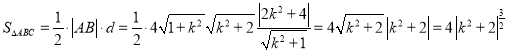
当![]() 时,
时,![]() 的面积最小,最小值为
的面积最小,最小值为![]()

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目